4) Over time, from measurements of the photometric and kinematic properties of normal galaxies, it became apparent that there exist correlations between the amount of motion of objects in the galaxy and the galaxy's luminosity. In this problem, we'll explore one of these relationships.
Spiral galaxies obey the Tully-Fisher Relation:
\begin{align}
L \sim v_{max}^4
\end{align}
where $L$ is total luminosity, and $v_{max}$ is the maximum observed rotational velocity. This relation was initially discovered observationally, but it is not hard to derive in a crude way:
(a) Assume that $v_{max} \sim \sigma$ (is this a good approximation?). Given what you know about the Virial Theorem, how should $v_{max}$ relate to the mass and radius of the Galaxy?
Using the Virial Theorem, we derived in problem 3 that the mass, radius, and stellar velocity can be related with the equation:
\begin{align}
M \approx \frac{\sigma^2 R}{G}
\end{align}
We can rearrange this equation to solve for $\sigma^2$ as follows:
\begin{align}
M \approx \frac{\sigma^2 R}{G}\\
\sigma^2 = \frac{M G}{R}
\end{align}
Let's assume that $v_{max} \sim \sigma$, which is a good assumption because we can think of $v_{max}$ as the average velocity of stars in the galaxy, and that they don't vary in speed too mych. Using this assumption, we can use the equation above to show the relationship between $v_{max}$ to the mass and radius of the galaxy as follows:
\begin{align}
v_{max}^2 \sim \frac{M}{R}
\end{align}
(b and c) To proceed from here, you need some handy observational facts. First, all spiral galaxies have a similar disk surface brightnesses ($\langle I \rangle = \frac{L}{R^2}$) (Freeman's Law). Second, they also have similar total mass-to-light ratios $(\frac{M}{L})$.
Use some squiggly math (drop the constants and use $\sim$ instead of $=$) to find the Tully-Fisher relationship.
Based on the Freeman's Law, we know that $\langle I \rangle = \frac{L}{R^2}$, which can be re-written as:
\begin{align}
I &= \frac{L}{R^2}\\
IR^2 &= L\\
R &\sim \sqrt{L}\\
\end{align}
Since we also know the mass-luminosity ratio as $\frac{M}{L}$, we can say that $M \sim L$.
We can plug these values for the $v_{max}$ derived in part (a) to get the Tully-Fisher Relation:
\begin{align}
v_{max}^2 &\sim \frac{M}{R} &\\
v_{max}^2 &\sim \frac{M}{\sqrt{L}} \rightarrow \text{Substituting for Freeman's Law}&\\
v_{max}^2 &\sim \frac{L}{\sqrt{L}} \rightarrow \text{Substituting for mass-ratio relation}&\\
v_{max}^2 &\sim \sqrt{L} &\\
v_{max}^4 &\sim L &\\
\end{align}
This is the Tully-Fisher Relation!
(d) It turns out the Tully-Fisher Relation is so well-obeyed that it can be used as a standard candle, just like the Cepheids and Supernova Ia seen previously. In the B-band ($\lambda_{cen} \sim 445$ nm, blue light), this relation is approximately:
\begin{align}
M_B = -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3
\end{align}
Suppose you observe a spiral galaxy with apparent, extinction-corrected magnitude B = 13 mag. You perform longslit optical spectroscopy, obtaining a maximum rotational velocity of 400 km/s for this galaxy. How distant do you infer this spiral galaxy to be?
We can calculate the distance of the spiral galaxy using its apparent and absolute magnitudes with the distance modulus equation:
\begin{align}
d = 10^{(\frac{m - M_B}{5} + 1)}
\end{align}
where $d$ is the distance to the spiral galaxy, $M_B$ is the absolute magnitude of the galaxy, and $m$ is the apparent magnitude of the galaxy. We are told that the apparent, extinction corrected magnitude is $m = B = 13$. Therefore, we just need to find the absolute magnitude of the galaxy.
We can solve for the absolute magnitude of the galaxy using the relation:
\begin{align}
M_B = -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3
\end{align}
where $M_B$ is the absolute magnitude of the galaxy, and $v_{max}$ is the maximum rotational velocity of this galaxy, which is told to be $v_{max}= 400$ km/s. We can plug in maximum rotational velocity into this equation to solve for the absolute magnitude, like so:
\begin{align}
M_B &= -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3\\
M_B &= -10 \log \left(\frac{400 \text{ km/s}}{\text{km/s}}\right) + 3\\
M_B &= -23
\end{align}
Now that we have both the apparent magnitude, $m = 13$ and the absolute magnitude, $M_B = -23$, we can plug these magnitudes into the distance modulus and solve for the distance, $d$ as follows:
\begin{align}
d &= 10^{(\frac{m - M_B}{5} + 1)}\\
d &= 10^{(\frac{13 + 23}{5} + 1)}\\
d &= 1.6 \times 10^8 \text{ pc}
\end{align}
Therefore, the spiral galaxy is $1.6 \times 10^8$ pc away!
Monday, October 19, 2015
Blog 17: Modeling Normal Galaxies Using the Virial Theorem
3) One of the most useful equations in astronomy is an extremely simple relationship known as the Virial Theorem. It can be used to derive Kepler's Third Law, measure the mass of a cluster of stars, or the temperature and brightness of a newly-formed planet. The Virial Theorem applies to a system of particles in equilibrium that are bound by a force that is defined by an inverse central-force law $(F \propto \frac{1}{r^\alpha})$. It relates the kinetic (or thermal) energy of a system $K$, to the potential energy, $U$, giving:
\begin{align}
k = -\frac{1}{2}U
\end{align}
(a) Consider a spherical distribution of $N$ particles, each with a mass $m$. The distribution has total mass $M$ and a total radius, $R$. Convince yourself that the total potential energy, $U$, is approximately
\begin{align}
U \approx -\frac{GM^2}{R}
\end{align}
You can derive or look up the actual numerical constant out front. But in general astronomy you don't need this prefactor, which is of order unity.
The total potential energy of the system can be modeled by the following equation:
\begin{align}
U = -\frac{G(\sum_{i = 1}^{N} m_i) (\sum_{j = 1}^{N} m_j)}{ r_{i,j}}
\end{align}
where $G$ is the gravitational constant, $m$ is the mass of a single particle in the spherical distribution, and $r$ is the radius between two particles, $i, j$ within a distribution of $N$ particles. Since there are $N$ particles, and the radius between two particles can be averaged out to the radius of the entire sphere, $R$, the equation above can be simplified to:
\begin{align}
U &= -\frac{G (N \times m) (N \times m)}{ R}\\
U &= -\frac{G N^2 m^2}{ R}\\
\end{align}
The total mass of the distribution, $M$ is the equivalent of the mass of a single particle, $m$, multiplied by the total number number of particles, $N$, given by the formula, $M = Nm$. We can substitute this into the previous equation to solve for the total potential energy as:
\begin{align}
U &= -\frac{G M^2}{ R}
\end{align}
However, the problem says that there should be a prefactor constant that is not included. Since it is a unity factor, it can be ignored, so the true potential energy can be modeled as:
\begin{align}
U \approx -\frac{G M^2}{ R}
\end{align}
(b) Now let's figure out what $K$ is equal to. Consider a bound spherical distribution of $N$ particles (perhaps stars in a globular cluster), each of mass $m$, and each moving away with a velocity of $v_i$ with respect to the center of mass. If these stars are far away in space, their individual velocity vectors are very difficult to measure directly. Generally, it is much easier to measure the scatter around the mean velocity if the system along our line of sight, the velocity scatter $\sigma^2$. Show that the kinetic energy of the system is:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
The equation for the total kinetic energy of a systemis:
\begin{align}
K = \frac{1}{2}M v^2
\end{align}
However, since the total mass $M$ is composite of the individual particle mass, $m$, times the total number of particles there are, $N$, $M = Nm$, and the equation for total kinetic energy can be written as:
\begin{align}
K = N \frac{1}{2}m v^2
\end{align}
Since the velocity scattering happens in a three dimensional frame, the velocity-squared of the system can be represented as:
\begin{align}
v^2 = 3 \sigma^2
\end{align}
Substituting this into the previous equation, you get a total kinetic energy of the system as:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
(c) Use the Virial Theorem to show that the total mass of, say, a globular cluster of radius $R$ and stellar velocity dispersion $\sigma$ is (to some prefactor of order unity):
\begin{align}
M \approx \frac{\sigma^2 R}{G}
\end{align}
Let's keep track of everything we know:
(1) The Virial Theorem:
\begin{align}
K = -\frac{1}{2}U
\end{align}
(2) The total kinetic energy of a system:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
(3) The total potential energy of a system:
\begin{align}
U \approx -\frac{G M^2}{ R}
\end{align}
(4) The relationship between the total mass, $M$, of a system, and the mass of a single particle of a system, $m$ for $N$ particles:
\begin{align}
M = Nm
\end{align}
Using this information, we can solve for the mass of the globular cluster, $M$, using the Virial Theorem, as follows:
\begin{align}
K &= -\frac{1}{2}U\\
N \frac{3}{2}m \sigma^2 &\approx -\frac{1}{2}\left(-\frac{G M^2}{ R}\right)\\
3 M \sigma^2 &\approx \frac{G M^2}{ R}\\
3 \sigma^2 &\approx \frac{G M}{ R}\\
\frac{3 \sigma^2 R}{G} &\approx M\\
M &\approx \frac{3 \sigma^2 R}{G}
\end{align}
We have derived an approximation for $M$ in terms of the velocity scatter $\sigma^2$, the radius $R$ of the globular cluster, and the gravitational constant $G$ as was intended. However, there is the coefficient 3 included that signifies the 3 dimensions of space. We can remove the coefficient to show the relationship as:
\begin{align}
M &\approx \frac{\sigma^2 R}{G}
\end{align}
Wednesday, October 7, 2015
Blog #16: The Great Debate (Shapley-Curtis Debate)
 |
| Harlow Shapley (left) and Heber Curtis (right) Source: http://education.ezinemark.com/top-10-science-debates-in-history-773690137c70.html |
At the heart of this debate was the question of the true scale of the Universe. Shapley asserted that Andromeda could not have been a separate galaxy because otherwise, by its apparent size and magnitude, it would have to be $10^8$ light years away. That distance seemed outlandish because it was further away than any other object in the Universe (based on the understanding at the time). Furthermore, astronomer Adriaan vas Maanen claimed that he measured what is now known as the Pinwheel Galaxy to be rotating within a timescale of years. Extrapolating the rate of rotation in the circumstance that the Pinwheel Galaxy was a separate galaxy would require the orbital velocity to be faster than the speed of light, thus defying the laws of physics. Finally, Shapley argued that he had observed a nova in the Andromeda "nebula" that outshone the entire nebula. Considering its brightness relative to all of Andromeda, if Andromeda was a separate galaxy, the amounts of energy release in the nova would be unimaginable.
Heber Curtis, however argued that it was strange that there were more "novas" inside the region marked as Andromeda, than at any other part of the Milky Way. This would suggest that Andromeda must be it's own galaxy far away. Curtis also cited dust clouds found in other galaxies similar to those in the Milky Way. Finally, he observed massive doppler shifts in objects he thought were galaxies, thus giving these galaxies a signature age that was different from that of the Milky Way.
However, the argument presented by Adriaan vas Maanen regarding the observation of rotating pinwheels in the Pinwheel Galaxy seemed to be the arbiter of the debate, since Curtis agreed that if the Pinwheel Galaxy was indeed rotating within an observational scale of years, then it would suggest that the orbital velocity of the galaxy was faster than the speed of light, and therefore his hypothesis would be wrong. It was later observed that, in fact, the rotation of the Pinwheel Galaxy could not be observed within the lifespan of humans, thus giving credibility to Curtis' argument.
Curtis' arguments were reconsidered when Edwin Hubble discovered Cepheid Variables in Andromeda and other "nebulae", which were calculated to be much further away than the Milky Way, suggesting that the Universe was, in fact, comprised of multiple galaxies, not just the Milky Way. Shapley's argument regarding the massively bright nova in Andromeda as having too much energy to be feasible was debunked when the existence of supernova was proven. Supernova do outside their respective galaxy, and are high-energy events measured in scales unimaginable in the early days of astronomy.
This debate provided the platform to discuss the "Scale of the Universe" to get a better insight of the immensity of the Universe we reside in. This debate showed how different points of view in astronomy were formulated based on the best information available at the time. Now we know that the Universe is filled with hundreds of billions of galaxies, and the Milky Way is just one of them.
Source: https://en.wikipedia.org/wiki/Great_Debate_(astronomy)
Monday, October 5, 2015
Blog #15: Worksheet 5.2- Cepheid Relations
Let's analyze real data about Cepheid Relations using Henrietta Swan Leavitt's actual date from 1908!
Included was a CSV file with the data.
(a) The data file, "Cepheid_variables.csv", contains data for 25 Cepheid variables located in the Small Magellanic Cloud (SMC). Each line contains a specific Cepheid's (1) ID number, (2) Maximum apparent magnitude, (3) Minimum apparent magnitude and (4) Period. Calculate the mean apparent magnitude for each Cepheid.
In order to find the mean apparent magnitude, I simply took the minimum and maximum apparent magnitudes of each Cepheid and averaged the two.
Since there were many individual Cepheids, I decided to get the mean apparent magnitude using Excel's "AVERAGE" function using the maximum and minimum apparent magnitudes as the input. The resulting mean apparent magnitude for each Cepheid is shown in the blue column in Table 1.
(b) The distance to the SMC is about 60 kpc, where kpc = 1000 pc. Convert your mean apparent magnitudes into mean absolute magnitudes. Plot the Cepheid mean absolute magnitudes as a function of period. This plot should look exponential.
In order to get the mean absolute magnitude, I had to convert the mean apparent magnitude into the mean absolute magnitude using the equation:
\begin{align}
M = m - 5 \log {\left(\frac{d}{10 \text{ pc}}\right)}
\end{align}
where $m$ is the mean apparent magnitude, and $d$ is the distance to the SMC, which is 6000 pc. The values of this conversion for each Cepheid to its mean absolute magnitude are in Table 1 in the orange column.
The plot looks as follows:
It does indeed look exponential.
(3) It is often handy to plot exponential (or power-law) functions with one or more logarithmic axes, which "straighten out" the data. Magnitudes are already exponential, so we don't need to adjust that axis. Plot the Cepheid mean absolute magnitudes as a function of $\log_{10}$(Period). Verify that the plot now looks linear.
In order to plot the mean absolute magnitude against a linear axis, I converted the period of each Cepheid into the log of the period, as shown in the purple column in Table 1, and got the following chart:
(4) and (5) Now that the data looks linear, we can estimate the parameters of the linear relation, $M_v(P) = A \log_{10}(\text{Period})+ B$. $A$ and $B$ are "free parameters" that allow the function to match the data.
You can determine the precise values of A and B by minimizing the difference between the observed points and model using the metric:
\begin{align}
\chi^2 \equiv \sum_{i=1}^{25}(O_i - C_i)^2
\end{align}
where $O_i$ is the observed value and $C_i$ is the predicted (model) value.
In this case, $A = -2.0332$ and $B = -2.7276$.
Included was a CSV file with the data.
(a) The data file, "Cepheid_variables.csv", contains data for 25 Cepheid variables located in the Small Magellanic Cloud (SMC). Each line contains a specific Cepheid's (1) ID number, (2) Maximum apparent magnitude, (3) Minimum apparent magnitude and (4) Period. Calculate the mean apparent magnitude for each Cepheid.
In order to find the mean apparent magnitude, I simply took the minimum and maximum apparent magnitudes of each Cepheid and averaged the two.
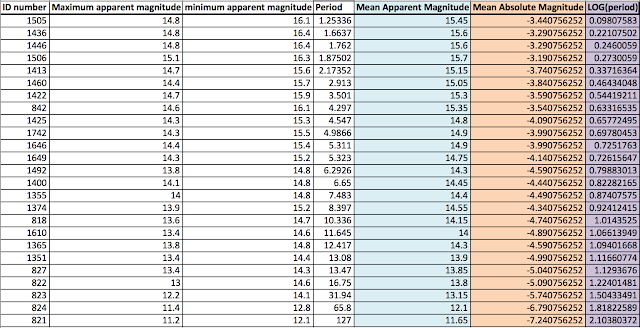 |
| Table 1: Cepheid Relations Chart |
(b) The distance to the SMC is about 60 kpc, where kpc = 1000 pc. Convert your mean apparent magnitudes into mean absolute magnitudes. Plot the Cepheid mean absolute magnitudes as a function of period. This plot should look exponential.
In order to get the mean absolute magnitude, I had to convert the mean apparent magnitude into the mean absolute magnitude using the equation:
\begin{align}
M = m - 5 \log {\left(\frac{d}{10 \text{ pc}}\right)}
\end{align}
where $m$ is the mean apparent magnitude, and $d$ is the distance to the SMC, which is 6000 pc. The values of this conversion for each Cepheid to its mean absolute magnitude are in Table 1 in the orange column.
The plot looks as follows:
 |
| Figure 1: Mean Absolute Magnitude vs. Period (days) |
It does indeed look exponential.
(3) It is often handy to plot exponential (or power-law) functions with one or more logarithmic axes, which "straighten out" the data. Magnitudes are already exponential, so we don't need to adjust that axis. Plot the Cepheid mean absolute magnitudes as a function of $\log_{10}$(Period). Verify that the plot now looks linear.
In order to plot the mean absolute magnitude against a linear axis, I converted the period of each Cepheid into the log of the period, as shown in the purple column in Table 1, and got the following chart:
 |
| Figure 2: Mean Absolute Magnitude vs. log(Period) in Days |
(4) and (5) Now that the data looks linear, we can estimate the parameters of the linear relation, $M_v(P) = A \log_{10}(\text{Period})+ B$. $A$ and $B$ are "free parameters" that allow the function to match the data.
You can determine the precise values of A and B by minimizing the difference between the observed points and model using the metric:
\begin{align}
\chi^2 \equiv \sum_{i=1}^{25}(O_i - C_i)^2
\end{align}
where $O_i$ is the observed value and $C_i$ is the predicted (model) value.
In this case, $A = -2.0332$ and $B = -2.7276$.
Blog #14: Worksheet 5.1 - Extragalactic Distance Ladder
(a) Suppose you are observing two stars, Star A and Star B. Star A is 3 magnitudes fainter than Star B. How much longer do you need to observe Star A to collect the same amount of energy in your detector as you do for Star B?
In order to relate the magnitudes of a star to their observation time, we need to look at how much light we are receiving per unit of time for each star. Flux is the measure of energy per time per area, and in this case, the "per area" is the same, since we are looking at the perceived flux reaching our eyes (or telescope if we are observing with a telescope). Since we are looking to see how much longer it will take for the light of Star A to reach us, we can use the proportion of fluxes of stars A and B using the relation:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)}
\end{align}
where in this case, the factor $(m_A - m_B)$ is the difference in magnitudes between Star A and Star B, which we know to be 3. Therefore, the ratio of fluxes of Star A and Star B is:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)} \approx 16
\end{align}
Since flux is related linearly with time, since the flux of Star A is 16 times less than the flux of Star B, it will take 16 times longer for Star A to collect the same amount of energy as Star B.
(b) Stars have both an apparent magnitude, $m$, which is how bright they appear from Earth. They also have an absolute magnitude, $\mathcal{M}$, which is the apparent magnitude a star would have at $d = 10$ pc. How does the apparent magnitude, $m$, of a star with absolute magnitude $\mathcal{M}$, depend on its distance, $d$ away from you?
Let's consider a star with an apparent magnitude, $m$, and an absolute magnitude, $\mathcal{M}$. The flux of the star is determined by the equation :
\begin{align}
F = \frac{\text{Luminosity}}{\text{Area}} = \frac{L}{\pi d^2}
\end{align}
where, L is the inherent luminosity of the star, and $d$ is the distance the star is away from you.
Knowing this, we can use the equation for the ratio of fluxes to determine the relationship between the apparent magnitude of a star, $m$ at a distance $d$, and the apparent magnitude of the same star if it were located $d = 10$ pc away.
The flux of the star at any given distance is:
\begin{align}
F_m = \frac{L}{4\pi d ^2}
\end{align}
The flux of a star at exactly $d = 10$ pc is as follows:
\begin{align}
F_M = \frac{L}{4\pi (10 \text{ pc}) ^2}
\end{align}
To solve for the relationship between the the apparent magnitude, $m$, and the absolute magnitude, $\mathcal{M}$ the ratio of the fluxes of these two values are as follows:
\begin{align}
\frac{F_{m}}{F_{M}} &= 10^{0.4(M - m)}\\
\frac{\frac{L}{4\pi d ^2}}{\frac{L}{4\pi (10 \text{ pc}) ^2}} &= 10^{0.4(M - m)}\\
\left(\frac{10 \text{ pc}}{d}\right)^2 &= 10^{0.4(M - m)}\\
\log{\left(\frac{10 \text{ pc}}{d}\right)^2} &= 0.4(M - m)\\
\frac{\log{\left(\frac{10 \text{ pc}}{d}\right)^2}}{0.4} &= M - m\\
m &= M - \frac{2 \log{\left(\frac{10 \text{ pc}}{d}\right)}}{0.4} \\
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}
\end{align}
This equation is known as the distance module, and the distance needs to be measured in parsecs.
(c) What is the star's parallax in terms of its apparent and absolute magnitudes?
The star's parallax with respect to its distance is given by the equation:
\begin{align}
\theta = \frac{1 \text{AU}}{d}
\end{align},
where, $theta$ is the parallax angle, and $d$ is the distance to the star, measured in parsecs.
We can use the equation derived in part (b) to solve for the distance, $d$, as follows:
\begin{align}
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
M - m &= 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
\frac{M - m}{5} &= \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
10^{\frac{M - m}{5}} &= \frac{10 \text{ pc}}{d}\\
d &= \frac{10^{0.2(M - m)}}{10 \text{ pc}}\\
\end{align}
Now that we have $d$ in terms of magnitudes, we can substitute it into the parallax equation above as follows:
\begin{align}
\theta &= \frac{1 \text{AU}}{d}\\
\theta &= \frac{1 \text{AU}}{\frac{10^{0.2(M - m)}}{10 \text{ pc}}}\\
\theta &= \frac{1 \text{AU}}{10^{0.2(M - m)}} \times 10 \text{ pc}
\end{align},
In order to relate the magnitudes of a star to their observation time, we need to look at how much light we are receiving per unit of time for each star. Flux is the measure of energy per time per area, and in this case, the "per area" is the same, since we are looking at the perceived flux reaching our eyes (or telescope if we are observing with a telescope). Since we are looking to see how much longer it will take for the light of Star A to reach us, we can use the proportion of fluxes of stars A and B using the relation:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)}
\end{align}
where in this case, the factor $(m_A - m_B)$ is the difference in magnitudes between Star A and Star B, which we know to be 3. Therefore, the ratio of fluxes of Star A and Star B is:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)} \approx 16
\end{align}
Since flux is related linearly with time, since the flux of Star A is 16 times less than the flux of Star B, it will take 16 times longer for Star A to collect the same amount of energy as Star B.
(b) Stars have both an apparent magnitude, $m$, which is how bright they appear from Earth. They also have an absolute magnitude, $\mathcal{M}$, which is the apparent magnitude a star would have at $d = 10$ pc. How does the apparent magnitude, $m$, of a star with absolute magnitude $\mathcal{M}$, depend on its distance, $d$ away from you?
Let's consider a star with an apparent magnitude, $m$, and an absolute magnitude, $\mathcal{M}$. The flux of the star is determined by the equation :
\begin{align}
F = \frac{\text{Luminosity}}{\text{Area}} = \frac{L}{\pi d^2}
\end{align}
where, L is the inherent luminosity of the star, and $d$ is the distance the star is away from you.
Knowing this, we can use the equation for the ratio of fluxes to determine the relationship between the apparent magnitude of a star, $m$ at a distance $d$, and the apparent magnitude of the same star if it were located $d = 10$ pc away.
The flux of the star at any given distance is:
\begin{align}
F_m = \frac{L}{4\pi d ^2}
\end{align}
The flux of a star at exactly $d = 10$ pc is as follows:
\begin{align}
F_M = \frac{L}{4\pi (10 \text{ pc}) ^2}
\end{align}
To solve for the relationship between the the apparent magnitude, $m$, and the absolute magnitude, $\mathcal{M}$ the ratio of the fluxes of these two values are as follows:
\begin{align}
\frac{F_{m}}{F_{M}} &= 10^{0.4(M - m)}\\
\frac{\frac{L}{4\pi d ^2}}{\frac{L}{4\pi (10 \text{ pc}) ^2}} &= 10^{0.4(M - m)}\\
\left(\frac{10 \text{ pc}}{d}\right)^2 &= 10^{0.4(M - m)}\\
\log{\left(\frac{10 \text{ pc}}{d}\right)^2} &= 0.4(M - m)\\
\frac{\log{\left(\frac{10 \text{ pc}}{d}\right)^2}}{0.4} &= M - m\\
m &= M - \frac{2 \log{\left(\frac{10 \text{ pc}}{d}\right)}}{0.4} \\
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}
\end{align}
This equation is known as the distance module, and the distance needs to be measured in parsecs.
(c) What is the star's parallax in terms of its apparent and absolute magnitudes?
The star's parallax with respect to its distance is given by the equation:
\begin{align}
\theta = \frac{1 \text{AU}}{d}
\end{align},
where, $theta$ is the parallax angle, and $d$ is the distance to the star, measured in parsecs.
We can use the equation derived in part (b) to solve for the distance, $d$, as follows:
\begin{align}
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
M - m &= 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
\frac{M - m}{5} &= \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
10^{\frac{M - m}{5}} &= \frac{10 \text{ pc}}{d}\\
d &= \frac{10^{0.2(M - m)}}{10 \text{ pc}}\\
\end{align}
Now that we have $d$ in terms of magnitudes, we can substitute it into the parallax equation above as follows:
\begin{align}
\theta &= \frac{1 \text{AU}}{d}\\
\theta &= \frac{1 \text{AU}}{\frac{10^{0.2(M - m)}}{10 \text{ pc}}}\\
\theta &= \frac{1 \text{AU}}{10^{0.2(M - m)}} \times 10 \text{ pc}
\end{align},
Subscribe to:
Comments (Atom)
