4) Over time, from measurements of the photometric and kinematic properties of normal galaxies, it became apparent that there exist correlations between the amount of motion of objects in the galaxy and the galaxy's luminosity. In this problem, we'll explore one of these relationships.
Spiral galaxies obey the Tully-Fisher Relation:
\begin{align}
L \sim v_{max}^4
\end{align}
where $L$ is total luminosity, and $v_{max}$ is the maximum observed rotational velocity. This relation was initially discovered observationally, but it is not hard to derive in a crude way:
(a) Assume that $v_{max} \sim \sigma$ (is this a good approximation?). Given what you know about the Virial Theorem, how should $v_{max}$ relate to the mass and radius of the Galaxy?
Using the Virial Theorem, we derived in problem 3 that the mass, radius, and stellar velocity can be related with the equation:
\begin{align}
M \approx \frac{\sigma^2 R}{G}
\end{align}
We can rearrange this equation to solve for $\sigma^2$ as follows:
\begin{align}
M \approx \frac{\sigma^2 R}{G}\\
\sigma^2 = \frac{M G}{R}
\end{align}
Let's assume that $v_{max} \sim \sigma$, which is a good assumption because we can think of $v_{max}$ as the average velocity of stars in the galaxy, and that they don't vary in speed too mych. Using this assumption, we can use the equation above to show the relationship between $v_{max}$ to the mass and radius of the galaxy as follows:
\begin{align}
v_{max}^2 \sim \frac{M}{R}
\end{align}
(b and c) To proceed from here, you need some handy observational facts. First, all spiral galaxies have a similar disk surface brightnesses ($\langle I \rangle = \frac{L}{R^2}$) (Freeman's Law). Second, they also have similar total mass-to-light ratios $(\frac{M}{L})$.
Use some squiggly math (drop the constants and use $\sim$ instead of $=$) to find the Tully-Fisher relationship.
Based on the Freeman's Law, we know that $\langle I \rangle = \frac{L}{R^2}$, which can be re-written as:
\begin{align}
I &= \frac{L}{R^2}\\
IR^2 &= L\\
R &\sim \sqrt{L}\\
\end{align}
Since we also know the mass-luminosity ratio as $\frac{M}{L}$, we can say that $M \sim L$.
We can plug these values for the $v_{max}$ derived in part (a) to get the Tully-Fisher Relation:
\begin{align}
v_{max}^2 &\sim \frac{M}{R} &\\
v_{max}^2 &\sim \frac{M}{\sqrt{L}} \rightarrow \text{Substituting for Freeman's Law}&\\
v_{max}^2 &\sim \frac{L}{\sqrt{L}} \rightarrow \text{Substituting for mass-ratio relation}&\\
v_{max}^2 &\sim \sqrt{L} &\\
v_{max}^4 &\sim L &\\
\end{align}
This is the Tully-Fisher Relation!
(d) It turns out the Tully-Fisher Relation is so well-obeyed that it can be used as a standard candle, just like the Cepheids and Supernova Ia seen previously. In the B-band ($\lambda_{cen} \sim 445$ nm, blue light), this relation is approximately:
\begin{align}
M_B = -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3
\end{align}
Suppose you observe a spiral galaxy with apparent, extinction-corrected magnitude B = 13 mag. You perform longslit optical spectroscopy, obtaining a maximum rotational velocity of 400 km/s for this galaxy. How distant do you infer this spiral galaxy to be?
We can calculate the distance of the spiral galaxy using its apparent and absolute magnitudes with the distance modulus equation:
\begin{align}
d = 10^{(\frac{m - M_B}{5} + 1)}
\end{align}
where $d$ is the distance to the spiral galaxy, $M_B$ is the absolute magnitude of the galaxy, and $m$ is the apparent magnitude of the galaxy. We are told that the apparent, extinction corrected magnitude is $m = B = 13$. Therefore, we just need to find the absolute magnitude of the galaxy.
We can solve for the absolute magnitude of the galaxy using the relation:
\begin{align}
M_B = -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3
\end{align}
where $M_B$ is the absolute magnitude of the galaxy, and $v_{max}$ is the maximum rotational velocity of this galaxy, which is told to be $v_{max}= 400$ km/s. We can plug in maximum rotational velocity into this equation to solve for the absolute magnitude, like so:
\begin{align}
M_B &= -10 \log \left(\frac{v_{max}}{\text{km/s}}\right) + 3\\
M_B &= -10 \log \left(\frac{400 \text{ km/s}}{\text{km/s}}\right) + 3\\
M_B &= -23
\end{align}
Now that we have both the apparent magnitude, $m = 13$ and the absolute magnitude, $M_B = -23$, we can plug these magnitudes into the distance modulus and solve for the distance, $d$ as follows:
\begin{align}
d &= 10^{(\frac{m - M_B}{5} + 1)}\\
d &= 10^{(\frac{13 + 23}{5} + 1)}\\
d &= 1.6 \times 10^8 \text{ pc}
\end{align}
Therefore, the spiral galaxy is $1.6 \times 10^8$ pc away!
Monday, October 19, 2015
Blog 17: Modeling Normal Galaxies Using the Virial Theorem
3) One of the most useful equations in astronomy is an extremely simple relationship known as the Virial Theorem. It can be used to derive Kepler's Third Law, measure the mass of a cluster of stars, or the temperature and brightness of a newly-formed planet. The Virial Theorem applies to a system of particles in equilibrium that are bound by a force that is defined by an inverse central-force law $(F \propto \frac{1}{r^\alpha})$. It relates the kinetic (or thermal) energy of a system $K$, to the potential energy, $U$, giving:
\begin{align}
k = -\frac{1}{2}U
\end{align}
(a) Consider a spherical distribution of $N$ particles, each with a mass $m$. The distribution has total mass $M$ and a total radius, $R$. Convince yourself that the total potential energy, $U$, is approximately
\begin{align}
U \approx -\frac{GM^2}{R}
\end{align}
You can derive or look up the actual numerical constant out front. But in general astronomy you don't need this prefactor, which is of order unity.
The total potential energy of the system can be modeled by the following equation:
\begin{align}
U = -\frac{G(\sum_{i = 1}^{N} m_i) (\sum_{j = 1}^{N} m_j)}{ r_{i,j}}
\end{align}
where $G$ is the gravitational constant, $m$ is the mass of a single particle in the spherical distribution, and $r$ is the radius between two particles, $i, j$ within a distribution of $N$ particles. Since there are $N$ particles, and the radius between two particles can be averaged out to the radius of the entire sphere, $R$, the equation above can be simplified to:
\begin{align}
U &= -\frac{G (N \times m) (N \times m)}{ R}\\
U &= -\frac{G N^2 m^2}{ R}\\
\end{align}
The total mass of the distribution, $M$ is the equivalent of the mass of a single particle, $m$, multiplied by the total number number of particles, $N$, given by the formula, $M = Nm$. We can substitute this into the previous equation to solve for the total potential energy as:
\begin{align}
U &= -\frac{G M^2}{ R}
\end{align}
However, the problem says that there should be a prefactor constant that is not included. Since it is a unity factor, it can be ignored, so the true potential energy can be modeled as:
\begin{align}
U \approx -\frac{G M^2}{ R}
\end{align}
(b) Now let's figure out what $K$ is equal to. Consider a bound spherical distribution of $N$ particles (perhaps stars in a globular cluster), each of mass $m$, and each moving away with a velocity of $v_i$ with respect to the center of mass. If these stars are far away in space, their individual velocity vectors are very difficult to measure directly. Generally, it is much easier to measure the scatter around the mean velocity if the system along our line of sight, the velocity scatter $\sigma^2$. Show that the kinetic energy of the system is:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
The equation for the total kinetic energy of a systemis:
\begin{align}
K = \frac{1}{2}M v^2
\end{align}
However, since the total mass $M$ is composite of the individual particle mass, $m$, times the total number of particles there are, $N$, $M = Nm$, and the equation for total kinetic energy can be written as:
\begin{align}
K = N \frac{1}{2}m v^2
\end{align}
Since the velocity scattering happens in a three dimensional frame, the velocity-squared of the system can be represented as:
\begin{align}
v^2 = 3 \sigma^2
\end{align}
Substituting this into the previous equation, you get a total kinetic energy of the system as:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
(c) Use the Virial Theorem to show that the total mass of, say, a globular cluster of radius $R$ and stellar velocity dispersion $\sigma$ is (to some prefactor of order unity):
\begin{align}
M \approx \frac{\sigma^2 R}{G}
\end{align}
Let's keep track of everything we know:
(1) The Virial Theorem:
\begin{align}
K = -\frac{1}{2}U
\end{align}
(2) The total kinetic energy of a system:
\begin{align}
K = N \frac{3}{2}m \sigma^2
\end{align}
(3) The total potential energy of a system:
\begin{align}
U \approx -\frac{G M^2}{ R}
\end{align}
(4) The relationship between the total mass, $M$, of a system, and the mass of a single particle of a system, $m$ for $N$ particles:
\begin{align}
M = Nm
\end{align}
Using this information, we can solve for the mass of the globular cluster, $M$, using the Virial Theorem, as follows:
\begin{align}
K &= -\frac{1}{2}U\\
N \frac{3}{2}m \sigma^2 &\approx -\frac{1}{2}\left(-\frac{G M^2}{ R}\right)\\
3 M \sigma^2 &\approx \frac{G M^2}{ R}\\
3 \sigma^2 &\approx \frac{G M}{ R}\\
\frac{3 \sigma^2 R}{G} &\approx M\\
M &\approx \frac{3 \sigma^2 R}{G}
\end{align}
We have derived an approximation for $M$ in terms of the velocity scatter $\sigma^2$, the radius $R$ of the globular cluster, and the gravitational constant $G$ as was intended. However, there is the coefficient 3 included that signifies the 3 dimensions of space. We can remove the coefficient to show the relationship as:
\begin{align}
M &\approx \frac{\sigma^2 R}{G}
\end{align}
Wednesday, October 7, 2015
Blog #16: The Great Debate (Shapley-Curtis Debate)
 |
| Harlow Shapley (left) and Heber Curtis (right) Source: http://education.ezinemark.com/top-10-science-debates-in-history-773690137c70.html |
At the heart of this debate was the question of the true scale of the Universe. Shapley asserted that Andromeda could not have been a separate galaxy because otherwise, by its apparent size and magnitude, it would have to be $10^8$ light years away. That distance seemed outlandish because it was further away than any other object in the Universe (based on the understanding at the time). Furthermore, astronomer Adriaan vas Maanen claimed that he measured what is now known as the Pinwheel Galaxy to be rotating within a timescale of years. Extrapolating the rate of rotation in the circumstance that the Pinwheel Galaxy was a separate galaxy would require the orbital velocity to be faster than the speed of light, thus defying the laws of physics. Finally, Shapley argued that he had observed a nova in the Andromeda "nebula" that outshone the entire nebula. Considering its brightness relative to all of Andromeda, if Andromeda was a separate galaxy, the amounts of energy release in the nova would be unimaginable.
Heber Curtis, however argued that it was strange that there were more "novas" inside the region marked as Andromeda, than at any other part of the Milky Way. This would suggest that Andromeda must be it's own galaxy far away. Curtis also cited dust clouds found in other galaxies similar to those in the Milky Way. Finally, he observed massive doppler shifts in objects he thought were galaxies, thus giving these galaxies a signature age that was different from that of the Milky Way.
However, the argument presented by Adriaan vas Maanen regarding the observation of rotating pinwheels in the Pinwheel Galaxy seemed to be the arbiter of the debate, since Curtis agreed that if the Pinwheel Galaxy was indeed rotating within an observational scale of years, then it would suggest that the orbital velocity of the galaxy was faster than the speed of light, and therefore his hypothesis would be wrong. It was later observed that, in fact, the rotation of the Pinwheel Galaxy could not be observed within the lifespan of humans, thus giving credibility to Curtis' argument.
Curtis' arguments were reconsidered when Edwin Hubble discovered Cepheid Variables in Andromeda and other "nebulae", which were calculated to be much further away than the Milky Way, suggesting that the Universe was, in fact, comprised of multiple galaxies, not just the Milky Way. Shapley's argument regarding the massively bright nova in Andromeda as having too much energy to be feasible was debunked when the existence of supernova was proven. Supernova do outside their respective galaxy, and are high-energy events measured in scales unimaginable in the early days of astronomy.
This debate provided the platform to discuss the "Scale of the Universe" to get a better insight of the immensity of the Universe we reside in. This debate showed how different points of view in astronomy were formulated based on the best information available at the time. Now we know that the Universe is filled with hundreds of billions of galaxies, and the Milky Way is just one of them.
Source: https://en.wikipedia.org/wiki/Great_Debate_(astronomy)
Monday, October 5, 2015
Blog #15: Worksheet 5.2- Cepheid Relations
Let's analyze real data about Cepheid Relations using Henrietta Swan Leavitt's actual date from 1908!
Included was a CSV file with the data.
(a) The data file, "Cepheid_variables.csv", contains data for 25 Cepheid variables located in the Small Magellanic Cloud (SMC). Each line contains a specific Cepheid's (1) ID number, (2) Maximum apparent magnitude, (3) Minimum apparent magnitude and (4) Period. Calculate the mean apparent magnitude for each Cepheid.
In order to find the mean apparent magnitude, I simply took the minimum and maximum apparent magnitudes of each Cepheid and averaged the two.
Since there were many individual Cepheids, I decided to get the mean apparent magnitude using Excel's "AVERAGE" function using the maximum and minimum apparent magnitudes as the input. The resulting mean apparent magnitude for each Cepheid is shown in the blue column in Table 1.
(b) The distance to the SMC is about 60 kpc, where kpc = 1000 pc. Convert your mean apparent magnitudes into mean absolute magnitudes. Plot the Cepheid mean absolute magnitudes as a function of period. This plot should look exponential.
In order to get the mean absolute magnitude, I had to convert the mean apparent magnitude into the mean absolute magnitude using the equation:
\begin{align}
M = m - 5 \log {\left(\frac{d}{10 \text{ pc}}\right)}
\end{align}
where $m$ is the mean apparent magnitude, and $d$ is the distance to the SMC, which is 6000 pc. The values of this conversion for each Cepheid to its mean absolute magnitude are in Table 1 in the orange column.
The plot looks as follows:
It does indeed look exponential.
(3) It is often handy to plot exponential (or power-law) functions with one or more logarithmic axes, which "straighten out" the data. Magnitudes are already exponential, so we don't need to adjust that axis. Plot the Cepheid mean absolute magnitudes as a function of $\log_{10}$(Period). Verify that the plot now looks linear.
In order to plot the mean absolute magnitude against a linear axis, I converted the period of each Cepheid into the log of the period, as shown in the purple column in Table 1, and got the following chart:
(4) and (5) Now that the data looks linear, we can estimate the parameters of the linear relation, $M_v(P) = A \log_{10}(\text{Period})+ B$. $A$ and $B$ are "free parameters" that allow the function to match the data.
You can determine the precise values of A and B by minimizing the difference between the observed points and model using the metric:
\begin{align}
\chi^2 \equiv \sum_{i=1}^{25}(O_i - C_i)^2
\end{align}
where $O_i$ is the observed value and $C_i$ is the predicted (model) value.
In this case, $A = -2.0332$ and $B = -2.7276$.
Included was a CSV file with the data.
(a) The data file, "Cepheid_variables.csv", contains data for 25 Cepheid variables located in the Small Magellanic Cloud (SMC). Each line contains a specific Cepheid's (1) ID number, (2) Maximum apparent magnitude, (3) Minimum apparent magnitude and (4) Period. Calculate the mean apparent magnitude for each Cepheid.
In order to find the mean apparent magnitude, I simply took the minimum and maximum apparent magnitudes of each Cepheid and averaged the two.
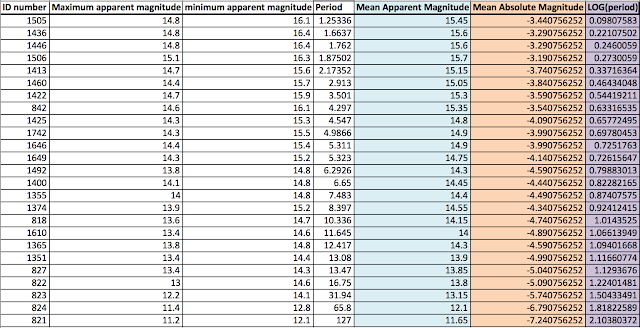 |
| Table 1: Cepheid Relations Chart |
(b) The distance to the SMC is about 60 kpc, where kpc = 1000 pc. Convert your mean apparent magnitudes into mean absolute magnitudes. Plot the Cepheid mean absolute magnitudes as a function of period. This plot should look exponential.
In order to get the mean absolute magnitude, I had to convert the mean apparent magnitude into the mean absolute magnitude using the equation:
\begin{align}
M = m - 5 \log {\left(\frac{d}{10 \text{ pc}}\right)}
\end{align}
where $m$ is the mean apparent magnitude, and $d$ is the distance to the SMC, which is 6000 pc. The values of this conversion for each Cepheid to its mean absolute magnitude are in Table 1 in the orange column.
The plot looks as follows:
 |
| Figure 1: Mean Absolute Magnitude vs. Period (days) |
It does indeed look exponential.
(3) It is often handy to plot exponential (or power-law) functions with one or more logarithmic axes, which "straighten out" the data. Magnitudes are already exponential, so we don't need to adjust that axis. Plot the Cepheid mean absolute magnitudes as a function of $\log_{10}$(Period). Verify that the plot now looks linear.
In order to plot the mean absolute magnitude against a linear axis, I converted the period of each Cepheid into the log of the period, as shown in the purple column in Table 1, and got the following chart:
 |
| Figure 2: Mean Absolute Magnitude vs. log(Period) in Days |
(4) and (5) Now that the data looks linear, we can estimate the parameters of the linear relation, $M_v(P) = A \log_{10}(\text{Period})+ B$. $A$ and $B$ are "free parameters" that allow the function to match the data.
You can determine the precise values of A and B by minimizing the difference between the observed points and model using the metric:
\begin{align}
\chi^2 \equiv \sum_{i=1}^{25}(O_i - C_i)^2
\end{align}
where $O_i$ is the observed value and $C_i$ is the predicted (model) value.
In this case, $A = -2.0332$ and $B = -2.7276$.
Blog #14: Worksheet 5.1 - Extragalactic Distance Ladder
(a) Suppose you are observing two stars, Star A and Star B. Star A is 3 magnitudes fainter than Star B. How much longer do you need to observe Star A to collect the same amount of energy in your detector as you do for Star B?
In order to relate the magnitudes of a star to their observation time, we need to look at how much light we are receiving per unit of time for each star. Flux is the measure of energy per time per area, and in this case, the "per area" is the same, since we are looking at the perceived flux reaching our eyes (or telescope if we are observing with a telescope). Since we are looking to see how much longer it will take for the light of Star A to reach us, we can use the proportion of fluxes of stars A and B using the relation:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)}
\end{align}
where in this case, the factor $(m_A - m_B)$ is the difference in magnitudes between Star A and Star B, which we know to be 3. Therefore, the ratio of fluxes of Star A and Star B is:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)} \approx 16
\end{align}
Since flux is related linearly with time, since the flux of Star A is 16 times less than the flux of Star B, it will take 16 times longer for Star A to collect the same amount of energy as Star B.
(b) Stars have both an apparent magnitude, $m$, which is how bright they appear from Earth. They also have an absolute magnitude, $\mathcal{M}$, which is the apparent magnitude a star would have at $d = 10$ pc. How does the apparent magnitude, $m$, of a star with absolute magnitude $\mathcal{M}$, depend on its distance, $d$ away from you?
Let's consider a star with an apparent magnitude, $m$, and an absolute magnitude, $\mathcal{M}$. The flux of the star is determined by the equation :
\begin{align}
F = \frac{\text{Luminosity}}{\text{Area}} = \frac{L}{\pi d^2}
\end{align}
where, L is the inherent luminosity of the star, and $d$ is the distance the star is away from you.
Knowing this, we can use the equation for the ratio of fluxes to determine the relationship between the apparent magnitude of a star, $m$ at a distance $d$, and the apparent magnitude of the same star if it were located $d = 10$ pc away.
The flux of the star at any given distance is:
\begin{align}
F_m = \frac{L}{4\pi d ^2}
\end{align}
The flux of a star at exactly $d = 10$ pc is as follows:
\begin{align}
F_M = \frac{L}{4\pi (10 \text{ pc}) ^2}
\end{align}
To solve for the relationship between the the apparent magnitude, $m$, and the absolute magnitude, $\mathcal{M}$ the ratio of the fluxes of these two values are as follows:
\begin{align}
\frac{F_{m}}{F_{M}} &= 10^{0.4(M - m)}\\
\frac{\frac{L}{4\pi d ^2}}{\frac{L}{4\pi (10 \text{ pc}) ^2}} &= 10^{0.4(M - m)}\\
\left(\frac{10 \text{ pc}}{d}\right)^2 &= 10^{0.4(M - m)}\\
\log{\left(\frac{10 \text{ pc}}{d}\right)^2} &= 0.4(M - m)\\
\frac{\log{\left(\frac{10 \text{ pc}}{d}\right)^2}}{0.4} &= M - m\\
m &= M - \frac{2 \log{\left(\frac{10 \text{ pc}}{d}\right)}}{0.4} \\
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}
\end{align}
This equation is known as the distance module, and the distance needs to be measured in parsecs.
(c) What is the star's parallax in terms of its apparent and absolute magnitudes?
The star's parallax with respect to its distance is given by the equation:
\begin{align}
\theta = \frac{1 \text{AU}}{d}
\end{align},
where, $theta$ is the parallax angle, and $d$ is the distance to the star, measured in parsecs.
We can use the equation derived in part (b) to solve for the distance, $d$, as follows:
\begin{align}
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
M - m &= 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
\frac{M - m}{5} &= \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
10^{\frac{M - m}{5}} &= \frac{10 \text{ pc}}{d}\\
d &= \frac{10^{0.2(M - m)}}{10 \text{ pc}}\\
\end{align}
Now that we have $d$ in terms of magnitudes, we can substitute it into the parallax equation above as follows:
\begin{align}
\theta &= \frac{1 \text{AU}}{d}\\
\theta &= \frac{1 \text{AU}}{\frac{10^{0.2(M - m)}}{10 \text{ pc}}}\\
\theta &= \frac{1 \text{AU}}{10^{0.2(M - m)}} \times 10 \text{ pc}
\end{align},
In order to relate the magnitudes of a star to their observation time, we need to look at how much light we are receiving per unit of time for each star. Flux is the measure of energy per time per area, and in this case, the "per area" is the same, since we are looking at the perceived flux reaching our eyes (or telescope if we are observing with a telescope). Since we are looking to see how much longer it will take for the light of Star A to reach us, we can use the proportion of fluxes of stars A and B using the relation:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)}
\end{align}
where in this case, the factor $(m_A - m_B)$ is the difference in magnitudes between Star A and Star B, which we know to be 3. Therefore, the ratio of fluxes of Star A and Star B is:
\begin{align}
\frac{F_{B}}{F_{A}} \approx 2.5^{(m_A - m_B)} \approx 16
\end{align}
Since flux is related linearly with time, since the flux of Star A is 16 times less than the flux of Star B, it will take 16 times longer for Star A to collect the same amount of energy as Star B.
(b) Stars have both an apparent magnitude, $m$, which is how bright they appear from Earth. They also have an absolute magnitude, $\mathcal{M}$, which is the apparent magnitude a star would have at $d = 10$ pc. How does the apparent magnitude, $m$, of a star with absolute magnitude $\mathcal{M}$, depend on its distance, $d$ away from you?
Let's consider a star with an apparent magnitude, $m$, and an absolute magnitude, $\mathcal{M}$. The flux of the star is determined by the equation :
\begin{align}
F = \frac{\text{Luminosity}}{\text{Area}} = \frac{L}{\pi d^2}
\end{align}
where, L is the inherent luminosity of the star, and $d$ is the distance the star is away from you.
Knowing this, we can use the equation for the ratio of fluxes to determine the relationship between the apparent magnitude of a star, $m$ at a distance $d$, and the apparent magnitude of the same star if it were located $d = 10$ pc away.
The flux of the star at any given distance is:
\begin{align}
F_m = \frac{L}{4\pi d ^2}
\end{align}
The flux of a star at exactly $d = 10$ pc is as follows:
\begin{align}
F_M = \frac{L}{4\pi (10 \text{ pc}) ^2}
\end{align}
To solve for the relationship between the the apparent magnitude, $m$, and the absolute magnitude, $\mathcal{M}$ the ratio of the fluxes of these two values are as follows:
\begin{align}
\frac{F_{m}}{F_{M}} &= 10^{0.4(M - m)}\\
\frac{\frac{L}{4\pi d ^2}}{\frac{L}{4\pi (10 \text{ pc}) ^2}} &= 10^{0.4(M - m)}\\
\left(\frac{10 \text{ pc}}{d}\right)^2 &= 10^{0.4(M - m)}\\
\log{\left(\frac{10 \text{ pc}}{d}\right)^2} &= 0.4(M - m)\\
\frac{\log{\left(\frac{10 \text{ pc}}{d}\right)^2}}{0.4} &= M - m\\
m &= M - \frac{2 \log{\left(\frac{10 \text{ pc}}{d}\right)}}{0.4} \\
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}
\end{align}
This equation is known as the distance module, and the distance needs to be measured in parsecs.
(c) What is the star's parallax in terms of its apparent and absolute magnitudes?
The star's parallax with respect to its distance is given by the equation:
\begin{align}
\theta = \frac{1 \text{AU}}{d}
\end{align},
where, $theta$ is the parallax angle, and $d$ is the distance to the star, measured in parsecs.
We can use the equation derived in part (b) to solve for the distance, $d$, as follows:
\begin{align}
m &= M - 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
M - m &= 5 \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
\frac{M - m}{5} &= \log{\left(\frac{10 \text{ pc}}{d}\right)}\\
10^{\frac{M - m}{5}} &= \frac{10 \text{ pc}}{d}\\
d &= \frac{10^{0.2(M - m)}}{10 \text{ pc}}\\
\end{align}
Now that we have $d$ in terms of magnitudes, we can substitute it into the parallax equation above as follows:
\begin{align}
\theta &= \frac{1 \text{AU}}{d}\\
\theta &= \frac{1 \text{AU}}{\frac{10^{0.2(M - m)}}{10 \text{ pc}}}\\
\theta &= \frac{1 \text{AU}}{10^{0.2(M - m)}} \times 10 \text{ pc}
\end{align},
Monday, September 28, 2015
Blog #13: Nathalie Cabrol, the Director for SETI
Nathalie Cabrol is an astrobiologist from France who studied at University of Paris in Nanterre as part of the Sorbonne, where she received her Ph.D in the field that is now known as planetary geology. Cabrol's work lies at the intersection of astronomy, geology, and biology as she attempts to intertwine these fields into the field of astrobiology. Cabrol has led the way in exploring uncharted territories in the search for extraterrestrial life by finding the limits of life on Earth. By exploring the harshest conditions on Earth, Cabrol has studied the extreme conditions in which life can ultimately survive.
As part of her studies as a planetary geologist, Cabrol's research focused on Gusev Crater on Mars. Through her expertise on Gusev Crater, one of Cabrol's signature achievements was to argue before NASA to choose Gusev Crater as a possible landing site for the Mars Exploration Rovers. In 2004, Gusev Crater was successfully chosen as the landing site for the rover Spirit.
After leaving NASA, Cabrol became the Principal Investigator and the expedition leader in the High Lakes Project. The High Lakes Project is an undertaking by SETI to understand the impact of extreme environmental stress on lake habitats and the effects of climate change in these habitats. As part of the project, Cabrol studied organisms that are prone to living in harsh conditions, called extremophiles, and saw that these organisms were thriving in conditions such as volcanic thermal vents, high irradiance and ultraviolet exposure, and dramatic pH changes due to the variable environment. Cabrol's research showed that regardless of how extreme the environment was, life seems to have evolved to adapt to any and all conditions. This is a profound discovery as it pertains to the possibility of life existing in other parts of the solar system, and the Universe as a whole.
Cabrol's research as a planetary geologist who studied planetary formations on Mars that could have been potential lake beds, along with her research on extremophiles in the High Lakes Project, make her uniquely suited to find analogues of conditions in the Universe that are hospitable to life with their Earth counterparts. As a result, in 2015, Cabrol became the director of the Carl Sagan Center at SETI, an organization aimed to answer the fundamental questions of the origin of life, and the possibility of life in other parts of the Universe.
Sources:
http://www.seti.org/users/nathalie-cabrol
https://astrobiology.nasa.gov/nai/reports/annual-reports/2008/seti/the-high-lakes-project-hlp/
http://www.seti.org/mos/nathalie-cabrol
Sunday, September 27, 2015
Blog #12: Say Cheese! Photographing light as a particle and a wave
We have all heard about the weird nature of elementary particles in the quantum world, especially the dual nature of light as both a particle and a wave.. Einstein's work on the photoelectric effect showed that light acts as discrete particles of light, called photons. However, other experiments, such as the double slit-experiment, shows light acting like, and having all the properties of a wave. Although at first this wave-particle duality was met with skepticism, today, it is accepted as fact.
However, although we now know that light acts as both a particle and a wave, the weird nature of quantum physics makes it so that the act of observing light determines whether or not you see its particulate properties, or its wave-like properties. We have never been able to see light act as both a particle and a wave at the same time!
This past year, however, scientists at the Swiss Federal Institute of Technology in Lausanne made headlines around the world after successfully capturing the first photograph of light acting as both a particle and a wave at the same time.
This image captures the wave nature of light as a $sinc()$ function. However, the shadow on the bottom of the picture shows discrete particles.
So how did these scientists manage to capture a photograph of light acting as both a particle and a wave, especially since you need light to take a photo in the first place?
Well, they used a classic imaging technique of using a beam of electrons and it's interaction with the object it is imaging, to take a picture of light. This technique is most notably used in electron microscopes, which give us the scarily up-close images of the microscopic world that are light microscopes are not able to see.
Okay, well things underneath an electron microscope are not moving, so we can take pictures of them. But light is always moving, so how do we keep it in one place to take a picture of it?
The scientists in Lausanne shot a beam of ultraviolet light onto a nano-wire. The UV light increased the energy of the wire, and caused a stream of photons to travel in opposite directions, creating a standing wave. In order to capture an image of this standing wave, the scientists shot a beam of electrons to see the light particles interact with the electrons, which was recorded to produce the first picture of light as both a particle and a wave!
This imaging technology can prove to be revolutionary, for it would allow scientists to image and even record the quantum world and it's effects directly. It could provide breakthroughs in fields like quantum computing, as well as help bridge the gap between the macro-world of stellar astronomy, and the quantum world.
For more information about this, check out this video:
Citation:
http://www.spacedaily.com/reports/The_first_ever_photograph_of_light_as_a_particle_and_a_wave_999.html
However, although we now know that light acts as both a particle and a wave, the weird nature of quantum physics makes it so that the act of observing light determines whether or not you see its particulate properties, or its wave-like properties. We have never been able to see light act as both a particle and a wave at the same time!
This past year, however, scientists at the Swiss Federal Institute of Technology in Lausanne made headlines around the world after successfully capturing the first photograph of light acting as both a particle and a wave at the same time.
This image captures the wave nature of light as a $sinc()$ function. However, the shadow on the bottom of the picture shows discrete particles.
So how did these scientists manage to capture a photograph of light acting as both a particle and a wave, especially since you need light to take a photo in the first place?
 |
| This is how the avian flu virus looks like under an electron microscope. Source: http://blog.silive.com/health/2008/10/avian-flu-virus.jpg |
Well, they used a classic imaging technique of using a beam of electrons and it's interaction with the object it is imaging, to take a picture of light. This technique is most notably used in electron microscopes, which give us the scarily up-close images of the microscopic world that are light microscopes are not able to see.
Okay, well things underneath an electron microscope are not moving, so we can take pictures of them. But light is always moving, so how do we keep it in one place to take a picture of it?
The scientists in Lausanne shot a beam of ultraviolet light onto a nano-wire. The UV light increased the energy of the wire, and caused a stream of photons to travel in opposite directions, creating a standing wave. In order to capture an image of this standing wave, the scientists shot a beam of electrons to see the light particles interact with the electrons, which was recorded to produce the first picture of light as both a particle and a wave!
This imaging technology can prove to be revolutionary, for it would allow scientists to image and even record the quantum world and it's effects directly. It could provide breakthroughs in fields like quantum computing, as well as help bridge the gap between the macro-world of stellar astronomy, and the quantum world.
For more information about this, check out this video:
Citation:
http://www.spacedaily.com/reports/The_first_ever_photograph_of_light_as_a_particle_and_a_wave_999.html
Blog #11: Microlensing
3) When speaking about microlensing, it is often easier to refer to angular quantities in units of $\theta_E$. Let's define $u \equiv \frac{\beta}{\theta_E}$ and $y \equiv \frac{\theta}{\theta_E}$.
(a) Show that the lens equation can be written as:
\begin{align}
u \equiv y - y^{-1}
\end{align}
Let's recall that the lens equation was obtained from Problem 2 and was defined as follows:
\begin{align} \beta = \theta - \alpha \end{align} This equation was later proved to be rewritten in part 2(d) as:
\begin{align}
\beta = \theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)
\end{align}
Therefore, we know that:
\begin{align}
\alpha' = \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)
\end{align}
All of this information will come in handy in just a minute. First, let's try to rewrite the lens equation in terms of $\theta_E$:
\begin{align}
\beta &= \theta - \alpha'\\
\frac{\beta}{\theta_E} &= \frac{\theta}{\theta_E} - \frac{\alpha'}{\theta_E}\\
\end{align}
In order to get the lens equation in the form $u = y - y^{-1}$, the following three conditions need to be true:
\begin{align}
(1) && u = \frac{\beta}{\theta_E}\\
(2) && y = \frac{\theta}{\theta_E}\\
(3) && y^{-1} = \frac{\alpha'}{\theta_E}
\end{align}
Since we don't know what $\theta_E$ is, we can't be sure if this relation will hold true if the three conditions above are met. So let's solve for $\theta_t$, given that $y^{-1} = \frac{\theta_E}{\theta}$ and $\alpha = \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)$ :
\begin{align}
y^{-1} &= \frac{\alpha'}{\theta_E}\\
\frac{\theta_E}{\theta} &= \frac{\alpha'}{\theta_E}\\
\theta_E^2 &= \alpha' \theta\\
\theta_E^2 &= \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right) \times \theta\\
\theta_E &= \left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}
\end{align}
In order to solve prove that the lens equation can be rewritten as $u = y-y^{-1}$, let's substitute this equation with the lens equation and see if it holds true:
\begin{align}
u &= y - y^{-1}\\
\frac{\beta}{\theta_E} &= \frac{\theta}{\theta_E} - \frac{\alpha'}{\theta_E}\\
\frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} &= \frac{\theta}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} - \frac{\frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}\\
\frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} &= \frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}
\end{align}
Since both sides equal to each other means that the three conditions above held true, and the lens equation can be re-written as $u = y - y^{-1}$.
(b) Solve for the roots of $y(u)$ in terms of $u$. These equations prescribe the angular position of the images as a function of the (mis)alignment between the source and lens. For the situation given in question 2(f) and a lens-source angular separation of 100 $\mu as$ (micro-arcseconds), indicate the position of the image in a drawing.
In order to solve for the roots of $y(u)$ in terms of $u$, we can look at the equation $u = y - y^{-1}$ and rewrite it and modify it to look like a polynomial equation as follows:
\begin{align}
u &= y - y^{-1}\\
0 &= y - y^{-1} - u\\
0(y) &= (y - y^{-1} - u) (y)\\
0 &= y^2 - uy - 1\\
\end{align}
Having the equation written in a polynomial form, we can solve for the roots of $y(u)$ in terms of $u$ using the quadratic formula as follows:
\begin{align}
y = \frac{u \pm \sqrt{u^2 + 4}}{2}
\end{align}
Now that we have an equation to get the two roots of $y$ in terms of $u$, let's try to calculate $u$. But before we try to calculate $u$, let's see what is all the information given to us:
We know from part (a) that $u = \frac{\beta}{\theta_E}$, and $\theta_E = \left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}$, which plug in the known values to solve for $u$:
\begin{align}
u &= \frac{\beta}{\theta_E}\\
u &= \frac{\beta}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{100 \mu as}{\left[ \frac{4(4.3 \times 10^{-3} \frac{\text{pc} \cdot \text{km}^2}{M_\odot \cdot s^2})(0.3 M_{\odot})}{(3 \times 10^5 \frac{\text{km}}{s})^2}\left(\frac{8000 \text{ pc} - 4000 \text{ pc}}{(8000 \text{ pc}) (4000 \text{ pc})}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{100 \mu as}{\left[ \frac{4(4.3 \times 10^{-3} \frac{\text{pc} \cdot \text{km}^2}{M_\odot \cdot s^2})(0.3 M_{\odot})}{(3 \times 10^5 \frac{\text{km}}{s})^2}\left(\frac{8000 \text{ pc} - 4000 \text{ pc}}{(8000 \text{ pc}) (4000 \text{ pc})}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{0.1 \text{ milli -arcseconds}}{2.7 \times 10^{-9} \text{ radians}}\\
u &= \frac{0.1 \text{ milli -arcseconds}}{0.6 \text{ milli-arcseconds}}\\
u &= 0.17 \text{ milli-arcseconds}
\end{align}
Now that we have solved for $u$, we can solve for the roots of $y(u)$ as follows:
\begin{align}
y &= \frac{u \pm \sqrt{u^2 + 4}}{2}\\
y &= \frac{0.17 \text{ milli-arcseconds}\pm \sqrt{(0.17 \text{ milli-arcseconds})^2 + 4}}{2}\\
y &= 1.09 \text{ milli-arcseconds}\\
&= -0.92 \text{ milli-arcseconds}
\end{align}
Okay, so now we have the 2 roots of $y$. One of them is a positive value and the other is a negative value. These two values have a real physical impact in how microlensing works. Look at the image below:
The positive value correlates to the larger, right side of the distorted image in the Einstein ring, and the negative value correlates to the smaller, left side of the distorted image in the Einstein ring. The positive and negatives indicates that the two images are mirror images of each other, with the positive value image being larger than the negative value image.
(a) Show that the lens equation can be written as:
\begin{align}
u \equiv y - y^{-1}
\end{align}
Let's recall that the lens equation was obtained from Problem 2 and was defined as follows:
\begin{align} \beta = \theta - \alpha \end{align} This equation was later proved to be rewritten in part 2(d) as:
\begin{align}
\beta = \theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)
\end{align}
Therefore, we know that:
\begin{align}
\alpha' = \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)
\end{align}
All of this information will come in handy in just a minute. First, let's try to rewrite the lens equation in terms of $\theta_E$:
\begin{align}
\beta &= \theta - \alpha'\\
\frac{\beta}{\theta_E} &= \frac{\theta}{\theta_E} - \frac{\alpha'}{\theta_E}\\
\end{align}
In order to get the lens equation in the form $u = y - y^{-1}$, the following three conditions need to be true:
\begin{align}
(1) && u = \frac{\beta}{\theta_E}\\
(2) && y = \frac{\theta}{\theta_E}\\
(3) && y^{-1} = \frac{\alpha'}{\theta_E}
\end{align}
Since we don't know what $\theta_E$ is, we can't be sure if this relation will hold true if the three conditions above are met. So let's solve for $\theta_t$, given that $y^{-1} = \frac{\theta_E}{\theta}$ and $\alpha = \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)$ :
\begin{align}
y^{-1} &= \frac{\alpha'}{\theta_E}\\
\frac{\theta_E}{\theta} &= \frac{\alpha'}{\theta_E}\\
\theta_E^2 &= \alpha' \theta\\
\theta_E^2 &= \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right) \times \theta\\
\theta_E &= \left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}
\end{align}
In order to solve prove that the lens equation can be rewritten as $u = y-y^{-1}$, let's substitute this equation with the lens equation and see if it holds true:
\begin{align}
u &= y - y^{-1}\\
\frac{\beta}{\theta_E} &= \frac{\theta}{\theta_E} - \frac{\alpha'}{\theta_E}\\
\frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} &= \frac{\theta}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} - \frac{\frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}\\
\frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}} &= \frac{\theta - \frac{4GM_L}{\theta c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}
\end{align}
Since both sides equal to each other means that the three conditions above held true, and the lens equation can be re-written as $u = y - y^{-1}$.
(b) Solve for the roots of $y(u)$ in terms of $u$. These equations prescribe the angular position of the images as a function of the (mis)alignment between the source and lens. For the situation given in question 2(f) and a lens-source angular separation of 100 $\mu as$ (micro-arcseconds), indicate the position of the image in a drawing.
In order to solve for the roots of $y(u)$ in terms of $u$, we can look at the equation $u = y - y^{-1}$ and rewrite it and modify it to look like a polynomial equation as follows:
\begin{align}
u &= y - y^{-1}\\
0 &= y - y^{-1} - u\\
0(y) &= (y - y^{-1} - u) (y)\\
0 &= y^2 - uy - 1\\
\end{align}
Having the equation written in a polynomial form, we can solve for the roots of $y(u)$ in terms of $u$ using the quadratic formula as follows:
\begin{align}
y = \frac{u \pm \sqrt{u^2 + 4}}{2}
\end{align}
Now that we have an equation to get the two roots of $y$ in terms of $u$, let's try to calculate $u$. But before we try to calculate $u$, let's see what is all the information given to us:
- $\beta = 100 \mu as = 0.1$ milli-arcseconds
- $M_L = 0.3 M_{\odot}$
- $D_L = 4 kpc = 4000 \text{ pc}$
- $D_S = 8 kpc = 8000 \text{ pc}$
- $G = 4.3 \times 10^{-3} \frac{\text{pc} \cdot \text{km}^2}{M_\odot \cdot s^2}$
- $c = 3 \times 10^5 \frac{\text{km}}{s}$
We know from part (a) that $u = \frac{\beta}{\theta_E}$, and $\theta_E = \left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}$, which plug in the known values to solve for $u$:
\begin{align}
u &= \frac{\beta}{\theta_E}\\
u &= \frac{\beta}{\left[ \frac{4GM_L}{c^2}\left(\frac{D_s - D_L}{D_S D_L}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{100 \mu as}{\left[ \frac{4(4.3 \times 10^{-3} \frac{\text{pc} \cdot \text{km}^2}{M_\odot \cdot s^2})(0.3 M_{\odot})}{(3 \times 10^5 \frac{\text{km}}{s})^2}\left(\frac{8000 \text{ pc} - 4000 \text{ pc}}{(8000 \text{ pc}) (4000 \text{ pc})}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{100 \mu as}{\left[ \frac{4(4.3 \times 10^{-3} \frac{\text{pc} \cdot \text{km}^2}{M_\odot \cdot s^2})(0.3 M_{\odot})}{(3 \times 10^5 \frac{\text{km}}{s})^2}\left(\frac{8000 \text{ pc} - 4000 \text{ pc}}{(8000 \text{ pc}) (4000 \text{ pc})}\right)\right]^{\frac{1}{2}}}\\
u &= \frac{0.1 \text{ milli -arcseconds}}{2.7 \times 10^{-9} \text{ radians}}\\
u &= \frac{0.1 \text{ milli -arcseconds}}{0.6 \text{ milli-arcseconds}}\\
u &= 0.17 \text{ milli-arcseconds}
\end{align}
Now that we have solved for $u$, we can solve for the roots of $y(u)$ as follows:
\begin{align}
y &= \frac{u \pm \sqrt{u^2 + 4}}{2}\\
y &= \frac{0.17 \text{ milli-arcseconds}\pm \sqrt{(0.17 \text{ milli-arcseconds})^2 + 4}}{2}\\
y &= 1.09 \text{ milli-arcseconds}\\
&= -0.92 \text{ milli-arcseconds}
\end{align}
Okay, so now we have the 2 roots of $y$. One of them is a positive value and the other is a negative value. These two values have a real physical impact in how microlensing works. Look at the image below:
The positive value correlates to the larger, right side of the distorted image in the Einstein ring, and the negative value correlates to the smaller, left side of the distorted image in the Einstein ring. The positive and negatives indicates that the two images are mirror images of each other, with the positive value image being larger than the negative value image.
Blog #10: Microlensing
1) Mass bends space-time! This is a prediction of general relativity, but fortunately we can heuristically derive the effect (up to a factor of 2) using Newtonian mechanics and some simplifying assumptions,
Consider a photon of "mass" $m_\gamma$ passing near an object of mass $M_L$; we'll call this object a "lens" (the 'L' in $M_L$ stands for "lens", which is the object doing the bending). The closest approach ($b$) of the photon is known as the impact parameter. We can imagine that the photon feels a gravitational acceleration from this lens, which we imagine is vertical (see diagram below:
(a) Give an expression for the gravitational acceleration in the vertical direction in terms of $M$, $b$, and $G$.
Okay, so we know that we are using basic Newtonian physics to solve for the distortion of space-time. Therefore, we can use basic Newtonian equations to solve for the gravitational acceleration in the vertical direction.
Recall that the relationship between force and acceleration can be described by Newton's Second Law of Motion:
\begin{align}
F = ma
\end{align}
Well in this case, we can use the force of gravitational acceleration, $F_g = \frac{GM_1M_2}{r^2}$, where the two masses, $M_1$ and $M_2$ are the mass of the "lens", $M_L$ and the "mass" of the photon, $m_{\gamma}$, respectively. The radius between the two bodies, $r$ is described by the variable $b$. Knowing this, we can rearrange Newton's second law and substitute in these variables for gravitational force, $F_g = \frac{G M_L M_\gamma}{b^2}$ in order to solve for the gravitational acceleration, $a$ as follows:
\begin{align}
F_g &= m_\gamma a\\
a &= \frac{F_g}{m}\\
a &= \frac{\frac{G M_L M_\gamma}{b^2}}{m_\gamma}\\
a &= \frac{G M_L}{b^2}\\
\end{align}
(b) Consider the time of interaction $\Delta t$. Assume that most of the influence the photon feels occurs in a horizontal distance $2b$. Express $\Delta t$ in terms of $b$ and the speed of the photon.
In order to solve for the "time of interaction", $\Delta t$, let's think about the direction that the photon was travelling. Since the photon was traveling in the horizontal direction, it feels the effects of gravity of $M_L$ the most over the horizontal distance, $2b$.
Since we know that the photon is traveling a distance of $2b$, and we are solving for the $\Delta t$, we can use the rudimentary knowledge of classical mechanics to relate the distance and time using the equation for velocity. Since velocity is measured as the distance traveled over a specified time, and we know that a photon travels at the speed of light, $c$, we can use the velocity equation to solve for $\Delta t$ as follows:
\begin{align}
v_{photon} &= \frac{\text{distance}}{\Delta t}\\
\Delta t &= \frac{\text{distance}}{v_{photon}}\\
\Delta t &= \frac{2b}{c}
\end{align}
(c) Solve for the change in velocity, $\Delta v$, in the direction perpendicular to the original photon path, over this time of interaction.
We are solving for the "change in velocity... over time of interaction", which sounds very much like the definition of acceleration ($a = \frac{\Delta v}{\Delta t}$)! Since the change in velocity, $\Delta v$, is happening over the distance perpendicular to the original photon path, we can use the acceleration derived in part (a) to solve for the change in velocity $\Delta v$. And since we are only measuring the "change in velocity", $\Delta v$ over the "time of interaction", $\Delta t$, we have all the necessary information to use the acceleration equation.
Recall that the acceleration in part (a) was $a = \frac{G M_L}{b^2}$, and the time of interaction, $\Delta t$ calculated in part (b) was $\Delta t = \frac{2b}{c}$. Using this information, we can rearrange the acceleration equation to solve for $\Delta v$ as follows:
\begin{align}
a &= \frac{\Delta v}{\Delta t}\\
\Delta v &= a \Delta t\\
\Delta v &= \frac{G M_L}{b^2} \times \frac{2b}{c}\\
\Delta v &= \frac{2G M_L}{bc}
\end{align}
(d) Now solve for the deflection angle ($\alpha$) in terms of $G$, $M_L$, $b$, and $c$ using your answer from part (a), (b), and (c). This result is a factor of 2 smaller than the correct, relativistic result.
According to the diagram above, the deflection angle $\alpha$ seems to create a right triangle with the horizontal and vertical components of the velocity of the path the photon is trying to take. Therefore, we can model the deflection angle as follows:
Using trigonometry, we can determine the following:
\begin{align}
\tan \alpha = \frac{\text{opposite}}{\text{adjacent}} = \frac{\Delta v}{c}
\end{align}
However, since the change in angle is very minute, we can use the small angle approximation to say that:
\begin{align}
\tan \alpha \approx \alpha = \frac{\Delta v}{c}
\end{align}
Since we can ignore the tangent function, we can solve for $\alpha$ using the equation above and the value calculated for $\Delta v = \frac{2G M_L}{bc}$ as follows:
\begin{align}
\alpha &= \frac{\Delta v}{c} \\
\alpha &= \frac{\frac{2G M_L}{bc}}{c} \\
\alpha &= \frac{2G M_L}{bc^2}
\end{align}
So now, we have the deflection angle, $\alpha$ using classical Newtonian mechanics. However, as the problem states, this answer is smaller than the actual answer obtained by general relativity by a factor of 2. Therefore, the correct relativistic deflective angle $\alpha$ is:
\begin{align}
\alpha = \frac{4G M_L}{bc^2}
\end{align}
Consider a photon of "mass" $m_\gamma$ passing near an object of mass $M_L$; we'll call this object a "lens" (the 'L' in $M_L$ stands for "lens", which is the object doing the bending). The closest approach ($b$) of the photon is known as the impact parameter. We can imagine that the photon feels a gravitational acceleration from this lens, which we imagine is vertical (see diagram below:
(a) Give an expression for the gravitational acceleration in the vertical direction in terms of $M$, $b$, and $G$.
Okay, so we know that we are using basic Newtonian physics to solve for the distortion of space-time. Therefore, we can use basic Newtonian equations to solve for the gravitational acceleration in the vertical direction.
Recall that the relationship between force and acceleration can be described by Newton's Second Law of Motion:
\begin{align}
F = ma
\end{align}
Well in this case, we can use the force of gravitational acceleration, $F_g = \frac{GM_1M_2}{r^2}$, where the two masses, $M_1$ and $M_2$ are the mass of the "lens", $M_L$ and the "mass" of the photon, $m_{\gamma}$, respectively. The radius between the two bodies, $r$ is described by the variable $b$. Knowing this, we can rearrange Newton's second law and substitute in these variables for gravitational force, $F_g = \frac{G M_L M_\gamma}{b^2}$ in order to solve for the gravitational acceleration, $a$ as follows:
\begin{align}
F_g &= m_\gamma a\\
a &= \frac{F_g}{m}\\
a &= \frac{\frac{G M_L M_\gamma}{b^2}}{m_\gamma}\\
a &= \frac{G M_L}{b^2}\\
\end{align}
(b) Consider the time of interaction $\Delta t$. Assume that most of the influence the photon feels occurs in a horizontal distance $2b$. Express $\Delta t$ in terms of $b$ and the speed of the photon.
In order to solve for the "time of interaction", $\Delta t$, let's think about the direction that the photon was travelling. Since the photon was traveling in the horizontal direction, it feels the effects of gravity of $M_L$ the most over the horizontal distance, $2b$.
Since we know that the photon is traveling a distance of $2b$, and we are solving for the $\Delta t$, we can use the rudimentary knowledge of classical mechanics to relate the distance and time using the equation for velocity. Since velocity is measured as the distance traveled over a specified time, and we know that a photon travels at the speed of light, $c$, we can use the velocity equation to solve for $\Delta t$ as follows:
\begin{align}
v_{photon} &= \frac{\text{distance}}{\Delta t}\\
\Delta t &= \frac{\text{distance}}{v_{photon}}\\
\Delta t &= \frac{2b}{c}
\end{align}
(c) Solve for the change in velocity, $\Delta v$, in the direction perpendicular to the original photon path, over this time of interaction.
We are solving for the "change in velocity... over time of interaction", which sounds very much like the definition of acceleration ($a = \frac{\Delta v}{\Delta t}$)! Since the change in velocity, $\Delta v$, is happening over the distance perpendicular to the original photon path, we can use the acceleration derived in part (a) to solve for the change in velocity $\Delta v$. And since we are only measuring the "change in velocity", $\Delta v$ over the "time of interaction", $\Delta t$, we have all the necessary information to use the acceleration equation.
Recall that the acceleration in part (a) was $a = \frac{G M_L}{b^2}$, and the time of interaction, $\Delta t$ calculated in part (b) was $\Delta t = \frac{2b}{c}$. Using this information, we can rearrange the acceleration equation to solve for $\Delta v$ as follows:
\begin{align}
a &= \frac{\Delta v}{\Delta t}\\
\Delta v &= a \Delta t\\
\Delta v &= \frac{G M_L}{b^2} \times \frac{2b}{c}\\
\Delta v &= \frac{2G M_L}{bc}
\end{align}
(d) Now solve for the deflection angle ($\alpha$) in terms of $G$, $M_L$, $b$, and $c$ using your answer from part (a), (b), and (c). This result is a factor of 2 smaller than the correct, relativistic result.
According to the diagram above, the deflection angle $\alpha$ seems to create a right triangle with the horizontal and vertical components of the velocity of the path the photon is trying to take. Therefore, we can model the deflection angle as follows:
Using trigonometry, we can determine the following:
\begin{align}
\tan \alpha = \frac{\text{opposite}}{\text{adjacent}} = \frac{\Delta v}{c}
\end{align}
However, since the change in angle is very minute, we can use the small angle approximation to say that:
\begin{align}
\tan \alpha \approx \alpha = \frac{\Delta v}{c}
\end{align}
Since we can ignore the tangent function, we can solve for $\alpha$ using the equation above and the value calculated for $\Delta v = \frac{2G M_L}{bc}$ as follows:
\begin{align}
\alpha &= \frac{\Delta v}{c} \\
\alpha &= \frac{\frac{2G M_L}{bc}}{c} \\
\alpha &= \frac{2G M_L}{bc^2}
\end{align}
So now, we have the deflection angle, $\alpha$ using classical Newtonian mechanics. However, as the problem states, this answer is smaller than the actual answer obtained by general relativity by a factor of 2. Therefore, the correct relativistic deflective angle $\alpha$ is:
\begin{align}
\alpha = \frac{4G M_L}{bc^2}
\end{align}
Monday, September 21, 2015
Blog #9: New Horizons Makes it to Pluto!!
New Horizons has made it to Pluto! And with it, we have uncovered a wealth of knowledge about the former planet never discovered before. What was once just a single pixel, the new high definition images of Pluto returned by New Horizons will literally write the textbooks for this little dwarf planet.
So, what do these images look like?

The Pictures:
The picture above is the true color image, while
the picture on the right uses an infrared filter to highlight certain geographical features.
One of the first things to note about these pictures is that neither of them are true color images, since New Horizons does not contain a green filter. Preliminary research about Pluto suggested that Pluto barely reflected any green light, so scientists opted to include an infrared filter instead, rendering the picture on the right. However, because Pluto does not reflect any green light, the image above, despite lacking a green filter, is the closest true-color image of Pluto that we have. In other words, if you were able to personally fly to Pluto to see it with your own eyes, it would look very similar to the image above.
The Spacecraft: New Horizons:
The spacecraft that travelled to Pluto for a flyby, New Horizons, was launched on January 19, 2006, when Pluto was still considered a planet to complete the tour of the Solar System following the two Voyager probes. New Horizons contains seven instruments, which included Ralph, Alice, REX, LORRI, SWAP, PEPSSI, and SDC. A quick breakdown of each of these instruments are as follows:
- Ralph: Visible and infrared imager/spectrometer. Provides color, composition, and thermal maps
- Alice: Ultraviolet imaging spectrometer. Analyzes composition of Pluto/Charon atmosphere
- REX (Radio Science EXperiment): Measures atmospheric composition and temperature. Passive radiometer.
- LORRI (Long Range Reconnaissance Imager): Telescopic camera .
- SWAP (Solar Wind Around Pluto): Solar wind and plasma spectrometer used to measure the effects of the solar wind on Pluto's atmosphere.
- PEPSSI (Pluto Energetic Particle Spectrometer Science Investigator): Measures composition and density of particles and plasma escaping from Pluto's atmosphere.
- SDS (Student Dust Counter): Tool designed and built by students to measure the space dust New Horizons encountered during its journey to Pluto.
The instruments on board New Horizons were designed to help scientists visualize and analyze Pluto in ways that were impossible to do so with space and ground based telescopes. One of the most impressive feats of the New Horizons mission was the speed at which the spacecraft was launched. To date, it is the fastest launch speed ever achieved. In fact, New Horizons is considered is considered the second fastest probe, only rivaled by the speed of Voyager 1. New Horizons achieved this speed and arrived at Pluto is such a relatively short time due to its relatively small mass, and a large boost from the Atlas V rocket launch system. The ion propulsion system did the majority of navigating through space, and a large gravity assist from Jupiter helped New Horizons achieve the speeds necessary to reach Pluto within 9 years.
On July 14th, 2015, New Horizons made its closest approach to Pluto, and used it's instruments to capture as much information as it could as it flew by the dwarf planet. New Horizons was never intended to stop and orbit Pluto due to the lack of fuel necessary to change its course. The spacecraft was moving too fast to ever slow down enough to enter the Pluto-Charon orbit, and was instead designed to gather as much information as possible during the fly-by. Now that the closest approach to Pluto has passed, NASA scientists hope to reroute the spacecraft as it goes through the Kuiper Belt to do a fly-by of a Kuiper Belt Object.
What we have learned:
The photos and other data returned by New Horizons have unveiled the mysteries of Pluto that were unknown due to the fact that ground and space based telescopes were not able to resolve Pluto to anything larger than a few pixels. However, looking at the pictures, it seems that Pluto has active geology that is shaping surface features, such as mountains made of methane and nitrogen ice as well as flat planes. Pluto is also confirmed to have polar ice caps. It is unclear as of yet what is causing the geological processes on the dwarf planet.
The color of Pluto, which appears to be a reddish brown color, is similar to that of Titan. The reddish brown is the result of an abundance of tholins. Tholins are organic compounds that form when cosmic rays and solar ultraviolet interact with methane. Since Pluto's thin atmosphere and surface is full of methane, the interaction with the solar wind and interstellar cosmic rays with the methane creates a chemical reaction the results in this reddish "gunk" that falls onto Pluto's surface, making it a reddish brown. Similar processes color Titan's surface, one of Saturn's moons with a thick methane atmosphere.
New Horizons wasn't just tasked with observing Pluto, but rather to get a better understanding of the Pluto-Charon system as a whole. Looking at Charon, it appears that Charon may also be geologically active. There are large crevices on the moon's surface, as well as fewer craters than expected. Also, Charon appears to have polar ice caps as well, with a large dark spot at its north pole.
Since New Horizons is still transmitting data back at the rate of 2 - 4 kb per second, it will take some time to get all of the data back. In the meantime, NASA is in the process to find a new Kuiper Belt Object to redirect New Horizons to in order to get a better understanding of the post Neptunian world.
Source:
http://www.nasa.gov/mission_pages/newhorizons/spacecraft/index.html
https://en.wikipedia.org/wiki/New_Horizons
Blog #8: Milky Way Rotation
5. $M(<r)$ is related to the mass density $\rho(r)$ by the integral:
\begin{align}
M(<r) = \int_{0}^{r} 4\pi r'^2 \rho (r')dr'
\end{align}
(Recall that the $4 \pi r'^2$ comes from the surface area of each spherical shell, and the $dr'$ is the thickness of each thin shell)
The fundamental theorem of calculus then implies that $4 \pi r^2 \rho(r) = \frac{dM(<r)}{dr}$. For the case in question 4, what is $\rho(r)$? Is the density finite as $r \rightarrow 0$ in the case of a flat rotation curve?
The case in question question 4 assumes that we have a flat rotation curve in the Milky Way galaxy, where the mass can be measured as a function of the radius, $r$, as $M(<r)$ with the following equation:
\begin{align}
M(<r) &= \frac{V_c^2 r}{G}
\end{align}
where, $V_c$ is the constant velocity, $r$ is the radius of the enclosed mass, $G$ is the universal gravitational constant.
Knowing $M(<r)$, we can use the equation derived from the fundamental theorem of calculus and solve for the density, $\rho(r)$ as follows:
\begin{align}
4 \pi r^2 \rho(r) &= \frac{dM(<r)}{dr}\\
4 \pi r^2 \rho(r) &= \frac{d\left(\frac{V_c^2 r}{G}\right)}{dr}\\
4 \pi r^2 \rho(r) &= \frac{dr\left(\frac{V_c^2}{G}\right)}{dr}\\
4 \pi r^2 \rho(r) &= \frac{V_c^2}{G}\\
\rho(r) &= \frac{V_c^2}{4 G \pi r^2 }
\end{align}
Now that we have solved for $\rho(r)$, we have to consider what happens when you get to the center of the galaxy, where $r \rightarrow 0$. As $r \rightarrow 0, \rho(r) \rightarrow \infty$, which is the point of singularity.
This shows that as you approach center of the Milky Way galaxy, the density is infinite, which is interesting, because right at the center of the Milky Way galaxy exists a supermassive black hole!
Blog #7: Milky Way Rotation
4. We actually observe a flat rotation curve in our own Milky Way. (You will show this with a radio telescope in your second lab!) This means that $v(r)$ is nearly constant for a larger range of distances.
(a) Let's call this constant rotational velocity $V_c$. If the mass distribution of the Milky Way is spherically symmetric, what must be the $M(<r)$ as a function of $r$ in this case, in terms of $V_c$, $r$, and $G$?
Since the rotation curve for the galaxy is actually flat, we can use the equation of Kepler's Rotation Curve derived in Blog#6, part(c) to solve for a the mass distribution. Recall that Kepler's Rotation curve is as follows:
\begin{align}
v(r) &= \left(\frac{GM_{enc}}{r}\right)^{\frac{1}{2}}
\end{align}
However, in this problem, since the enclosed mass, $M_{enc}$ is a function of radius, $r$, and the velocity is constant, $V_c$, we can rewrite the equation as follows:
\begin{align}
V_c &= \left(\frac{GM(<r)}{r}\right)^{\frac{1}{2}}
\end{align}
Since we are looking for $M(<r)$, we can rearrange the equation to solve for $M(<r)$:
\begin{align}
V_c &= \left(\frac{GM(<r)}{r}\right)^{\frac{1}{2}}\\
V_c^2 &= \frac{GM(<r)}{r}\\
M(<r) &= \frac{V_c^2 r}{G}
\end{align}
(b) How does this compare with the picture of the galaxy you drew last week with most of the mass appearing to be in bulge?
Looking at mass as function of radius, $M(<r) = \frac{V_c^2 r}{G}$, you can see that this equation implies that mass increases linearly the further away you go from the center of the galaxy. However, this shows that mass and radius have a linear relationship, meaning that the volume has to increase linearly. However, volume does not increase linearly in a spherical configuration. Therefore, looking at the galaxy as a cylinder, we can think of the height of the cylinder as the radius, which would increase volume linearly with a constant of $\pi r^2$. Therefore, this shows that the mass of the galaxy cannot be concentrated in a bulge, but rather in a more cylindrical shape.
(c) If the Milky Way rotation curve is observed to be flat ($V_c \approx 240$ km/s) out of 100 kpc, what is the total mass enclosed within 100 kpc? How does this compare with the mass in stars?
We can solve for total mass enclosed within 100 kpc of the galaxy by plugging in values into the equation derived in part (a) as follows:
\begin{align}
M(<r) &= \frac{V_c^2 r}{G}\\
M(<r) &= \frac{(240 \frac{km}{s})^2 (100 \text{ kpc})}{4.3 \times 10^{-3} \frac{\text{ pc} \cdot \text{km}^2}{M_{\odot}\text{s}^2}}\\
M(<r) &= \frac{(240 \frac{km}{s})^2 (1 \times 10^5 \text{ pc})}{4.3 \times 10^{-3} \frac{\text{ pc} \cdot \text{km}^2}{M_{\odot}\text{s}^2}}\\
M(<r) &= 1.3 \times 10^{12} M_{\odot}
\end{align}
The mass of the Milky Way comes out to be $1.3 \times 10^{12} M_{\odot}$, which is huge! What is more interesting is that we know that the stellar mass of the Milky Way is about $10^{10} M_{\odot}$. If we subtract the stellar mass of the Milky Way with the mass of the entire Milky Way galaxy, $1.3 \times 10^{12} M_{\odot} - 10^{10} M_{\odot} = 1.29 \times 10^{12}$.
Therefore, stars make up only 1% of the mass of the Milky Way!
(a) Let's call this constant rotational velocity $V_c$. If the mass distribution of the Milky Way is spherically symmetric, what must be the $M(<r)$ as a function of $r$ in this case, in terms of $V_c$, $r$, and $G$?
Since the rotation curve for the galaxy is actually flat, we can use the equation of Kepler's Rotation Curve derived in Blog#6, part(c) to solve for a the mass distribution. Recall that Kepler's Rotation curve is as follows:
\begin{align}
v(r) &= \left(\frac{GM_{enc}}{r}\right)^{\frac{1}{2}}
\end{align}
However, in this problem, since the enclosed mass, $M_{enc}$ is a function of radius, $r$, and the velocity is constant, $V_c$, we can rewrite the equation as follows:
\begin{align}
V_c &= \left(\frac{GM(<r)}{r}\right)^{\frac{1}{2}}
\end{align}
Since we are looking for $M(<r)$, we can rearrange the equation to solve for $M(<r)$:
\begin{align}
V_c &= \left(\frac{GM(<r)}{r}\right)^{\frac{1}{2}}\\
V_c^2 &= \frac{GM(<r)}{r}\\
M(<r) &= \frac{V_c^2 r}{G}
\end{align}
(b) How does this compare with the picture of the galaxy you drew last week with most of the mass appearing to be in bulge?
Looking at mass as function of radius, $M(<r) = \frac{V_c^2 r}{G}$, you can see that this equation implies that mass increases linearly the further away you go from the center of the galaxy. However, this shows that mass and radius have a linear relationship, meaning that the volume has to increase linearly. However, volume does not increase linearly in a spherical configuration. Therefore, looking at the galaxy as a cylinder, we can think of the height of the cylinder as the radius, which would increase volume linearly with a constant of $\pi r^2$. Therefore, this shows that the mass of the galaxy cannot be concentrated in a bulge, but rather in a more cylindrical shape.
(c) If the Milky Way rotation curve is observed to be flat ($V_c \approx 240$ km/s) out of 100 kpc, what is the total mass enclosed within 100 kpc? How does this compare with the mass in stars?
We can solve for total mass enclosed within 100 kpc of the galaxy by plugging in values into the equation derived in part (a) as follows:
\begin{align}
M(<r) &= \frac{V_c^2 r}{G}\\
M(<r) &= \frac{(240 \frac{km}{s})^2 (100 \text{ kpc})}{4.3 \times 10^{-3} \frac{\text{ pc} \cdot \text{km}^2}{M_{\odot}\text{s}^2}}\\
M(<r) &= \frac{(240 \frac{km}{s})^2 (1 \times 10^5 \text{ pc})}{4.3 \times 10^{-3} \frac{\text{ pc} \cdot \text{km}^2}{M_{\odot}\text{s}^2}}\\
M(<r) &= 1.3 \times 10^{12} M_{\odot}
\end{align}
The mass of the Milky Way comes out to be $1.3 \times 10^{12} M_{\odot}$, which is huge! What is more interesting is that we know that the stellar mass of the Milky Way is about $10^{10} M_{\odot}$. If we subtract the stellar mass of the Milky Way with the mass of the entire Milky Way galaxy, $1.3 \times 10^{12} M_{\odot} - 10^{10} M_{\odot} = 1.29 \times 10^{12}$.
Therefore, stars make up only 1% of the mass of the Milky Way!
Blog #6: Milky Way Rotation
3) Last time we approximated the shape of our Galaxy as a cylinder. This time it will be a sphere. If there are no other large-scale forces other than gravity (a good approximation in most galaxies), then an object's orbit around the galactic center will be the approximate center.
(a) Show that Kepler's 3rd can be expressed in terms of the orbital frequency $\Omega \equiv \frac{2 \pi}{P}$ (i. e. orbits/time) and the distance from the center
\begin{align}
r^3 \Omega^2 \equiv G M_{tot}
\end{align}
Knowing that the orbital frequency $\Omega \equiv \frac{2 \pi}{P}$, we can rearrange it to solve for the period, $P = \frac{2\pi}{\Omega}$. Now that we have period, $P$, in terms of orbital frequency $\Omega$, we can substitute it into the equation for Kepler's Third Law to get Kepler's Third Law in terms of orbital period as follows:
\begin{align}
P^2 &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\left( \frac{2\pi}{\Omega}\right)^2 &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\frac{4 \pi^2}{\Omega^2} &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\frac{1}{\Omega^2} &= \frac{ r^3}{GM_{tot}}\\
\Omega^2 r^3 &= GM_{tot}
\end{align}
(b) Now, assume that the Milky Way has a spherical mass distribution - this is a good approximation when talking about the total mass distribution. Using what you learned from Problem 2, rewrite the above for an object orbiting a radius $r$ from the center of the galaxy.
Assuming that the Milky Way has a spherical mass distribution implies that the total mass that is being considered is a function of how far from the center of the sphere you are at.
Basically, at any given radius $r$ from the center of the sphere, the total mass that is enclosed in that mass, $M_{enc}$ includes the gravitational effects of the total mass enclosed within that radius, and is not affected by any mass beyond that radius.
Therefore, you can rewrite the equation is part (a) to the following:
\begin{align}
\Omega^2 r^3 &= GM_{enc}
\end{align}
(c) Next, let's call the velocity of this object at distance $r$ away from the center, $v(r)$. Use Kepler's Third Law as expressed above to derive $v(r)$ for a mass $m$ if the central mass is concentrated in a single point at the center (with mass $M_{enc}$), in terms of $M_{enc}$, $G$, and $r$. This is known as the Keplerian rotation curve. As you saw earlier, it describes the motion of the planets in the solar system, since the Sun has nearly all of the mass.
So far, the equations we have about orbital period and Kepler's Third Law are:
\begin{align}
(1) & \Omega^2 r^3 = GM_{enc}\\
(2) & \Omega = \frac{2 \pi}{P}
\end{align}
In order to relate these two by velocity as a function of radius, $v(r)$, we need to think about rotational velocity. Since velocity is defined as $v = \frac{\text{distance}}{\text{time}}$, we can think of the circumference of an orbit, $2\pi r$ as the distance, and the period of the orbit, $P$, as the time, which gives us:
\begin{align}
v(r) = \frac{2 \pi r}{P}
\end{align}
Knowing these equations, we can solve for orbital period, $\Omega$ in terms of $v(r)$ as follows:
\begin{align}
\Omega = \frac{2 \pi}{P} &\text{ and } v(r) = \frac{2 \pi r}{P}\\
v(r) &= \Omega r\\
\Omega &= \frac{v(r)}{r}
\end{align}
Finally, we can substitute this equation into Kepler's Third Law in terms of orbital velocity to find Kepler's Rotation Curve as follows:
\begin{align}
\Omega^2 r^3 &= GM_{enc}\\
(\frac{v(r)}{r})^2 r^3 &= GM_{enc}\\
v(r)^2 r &= GM_{enc}\\
v(r) &= \left(\frac{GM_{enc}}{r}\right)^{\frac{1}{2}}
\end{align}
(a) Show that Kepler's 3rd can be expressed in terms of the orbital frequency $\Omega \equiv \frac{2 \pi}{P}$ (i. e. orbits/time) and the distance from the center
\begin{align}
r^3 \Omega^2 \equiv G M_{tot}
\end{align}
Knowing that the orbital frequency $\Omega \equiv \frac{2 \pi}{P}$, we can rearrange it to solve for the period, $P = \frac{2\pi}{\Omega}$. Now that we have period, $P$, in terms of orbital frequency $\Omega$, we can substitute it into the equation for Kepler's Third Law to get Kepler's Third Law in terms of orbital period as follows:
\begin{align}
P^2 &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\left( \frac{2\pi}{\Omega}\right)^2 &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\frac{4 \pi^2}{\Omega^2} &= \frac{4\pi^2 r^3}{GM_{tot}}\\
\frac{1}{\Omega^2} &= \frac{ r^3}{GM_{tot}}\\
\Omega^2 r^3 &= GM_{tot}
\end{align}
(b) Now, assume that the Milky Way has a spherical mass distribution - this is a good approximation when talking about the total mass distribution. Using what you learned from Problem 2, rewrite the above for an object orbiting a radius $r$ from the center of the galaxy.
Assuming that the Milky Way has a spherical mass distribution implies that the total mass that is being considered is a function of how far from the center of the sphere you are at.
Basically, at any given radius $r$ from the center of the sphere, the total mass that is enclosed in that mass, $M_{enc}$ includes the gravitational effects of the total mass enclosed within that radius, and is not affected by any mass beyond that radius.
Therefore, you can rewrite the equation is part (a) to the following:
\begin{align}
\Omega^2 r^3 &= GM_{enc}
\end{align}
(c) Next, let's call the velocity of this object at distance $r$ away from the center, $v(r)$. Use Kepler's Third Law as expressed above to derive $v(r)$ for a mass $m$ if the central mass is concentrated in a single point at the center (with mass $M_{enc}$), in terms of $M_{enc}$, $G$, and $r$. This is known as the Keplerian rotation curve. As you saw earlier, it describes the motion of the planets in the solar system, since the Sun has nearly all of the mass.
So far, the equations we have about orbital period and Kepler's Third Law are:
\begin{align}
(1) & \Omega^2 r^3 = GM_{enc}\\
(2) & \Omega = \frac{2 \pi}{P}
\end{align}
In order to relate these two by velocity as a function of radius, $v(r)$, we need to think about rotational velocity. Since velocity is defined as $v = \frac{\text{distance}}{\text{time}}$, we can think of the circumference of an orbit, $2\pi r$ as the distance, and the period of the orbit, $P$, as the time, which gives us:
\begin{align}
v(r) = \frac{2 \pi r}{P}
\end{align}
Knowing these equations, we can solve for orbital period, $\Omega$ in terms of $v(r)$ as follows:
\begin{align}
\Omega = \frac{2 \pi}{P} &\text{ and } v(r) = \frac{2 \pi r}{P}\\
v(r) &= \Omega r\\
\Omega &= \frac{v(r)}{r}
\end{align}
Finally, we can substitute this equation into Kepler's Third Law in terms of orbital velocity to find Kepler's Rotation Curve as follows:
\begin{align}
\Omega^2 r^3 &= GM_{enc}\\
(\frac{v(r)}{r})^2 r^3 &= GM_{enc}\\
v(r)^2 r &= GM_{enc}\\
v(r) &= \left(\frac{GM_{enc}}{r}\right)^{\frac{1}{2}}
\end{align}
Sunday, September 13, 2015
Blog #5: Is that a Supernova?
4) A supernova goes off and you can barely detect it with your eyes. Astronomers tell you that supernovae have a luminosity of $10^{42} \frac{\text{ ergs}}{\text{ second}}$. What is the distance of the supernova?
Assume the supernova emits most of its energy at the peak of the eye's sensitivity and that it explodes isotropically.
In order to solve this problem, let's consider what it means for a supernova to be barely detectable with their eyes. Since the light is barely being received by the eye, it means that even the faintest appearance of the supernova would make the eye receives at least 10 photons of light with a framerate of about 60 frames per second. Also important to note is that humans see the average wavelength of 600 nm. This information can tell us how much power the eye inputs in order to see this image.
Power is defined as units of energy over time. Energy of one photon is defined as $E = \frac{hc}{\lambda}$, where $h = 6.62 \times 10^{-27} \frac{erg}{sec}$ is planck's constant, $c = 3 \times 10^{10} \frac{cm}{sec}$ is the speed of light, and $\lambda = 6 \times 10^{-5}$ is the wavelength. Using this information, the power int of the eye is:
\begin{align}
P_{eye} &= \frac{\text{Energy of 10 Photons}}{\text{time}}\\
P_{eye} &= \frac{10 \times \frac{hc}{\lambda}}{\frac{1}{60 \text{ sec}}}\\
P_{eye} &= \frac{10 \times hc \times 60}{\lambda}\\
P_{eye} &= \frac{(10) \times (6.62 \times 10^{-27} \frac{\text{ erg}}{\text{ sec}}) \times (3 \times 10^{10} \frac{\text{ cm}}{\text{ sec}})\times (60 \text{ sec})}{6 \times 10^{-5} \text{cm}}\\
P_{eye} &\approx 2 \times 10^{-9} \frac{ \text{ ergs}}{\text{ sec}}
\end{align}
Now that we know how much power the eye is inputting, we can set up a proportion to compare the surface area of the eye, $SA_{eye}$ and the surface area of the $SA_{supernova}$ with the power input of the eye, $P_{eye}$, with the power output of the supernova, $P_{supernova}$. The proportion is as follows:
\begin{align}
\frac{P_{supernova}}{SA_{supernova}} &= \frac{P_{eye}}{SA_{eye}}\\
\frac{P_{supernova}}{4\pi D^2} &= \frac{P_{eye}}{4\pi R_{eye}^2}
\end{align}
Having this proportionality, we can rearrange the equation above to solve for the distance to the supernova. Assume that the radius of the eye is about 1 cm.
\begin{align}
\frac{P_{supernova}}{4\pi D^2} &= \frac{P_{eye}}{4\pi R_{eye}^2}\\
D &= \left(\frac{R_{eye}^2 \times P_{supernova}}{4 P_{eye}}\right)^{\frac{1}{2}}\\
D &= \left(\frac{(1 \text{ cm})^2 \times (10^{42} \frac{\text{ ergs}}{\text{ second}})}{4 \times (2 \times 10^{-9} \frac{ \text{ ergs}}{\text{ sec}})}\right)^{\frac{1}{2}}\\
D &= 1.12 \times 10^{25} \text{ cm}
\end{align}
Therefore, the supernova exploded $1.12 \times 10^{25} \text{ cm}$ away!!!
Assume the supernova emits most of its energy at the peak of the eye's sensitivity and that it explodes isotropically.
In order to solve this problem, let's consider what it means for a supernova to be barely detectable with their eyes. Since the light is barely being received by the eye, it means that even the faintest appearance of the supernova would make the eye receives at least 10 photons of light with a framerate of about 60 frames per second. Also important to note is that humans see the average wavelength of 600 nm. This information can tell us how much power the eye inputs in order to see this image.
Power is defined as units of energy over time. Energy of one photon is defined as $E = \frac{hc}{\lambda}$, where $h = 6.62 \times 10^{-27} \frac{erg}{sec}$ is planck's constant, $c = 3 \times 10^{10} \frac{cm}{sec}$ is the speed of light, and $\lambda = 6 \times 10^{-5}$ is the wavelength. Using this information, the power int of the eye is:
\begin{align}
P_{eye} &= \frac{\text{Energy of 10 Photons}}{\text{time}}\\
P_{eye} &= \frac{10 \times \frac{hc}{\lambda}}{\frac{1}{60 \text{ sec}}}\\
P_{eye} &= \frac{10 \times hc \times 60}{\lambda}\\
P_{eye} &= \frac{(10) \times (6.62 \times 10^{-27} \frac{\text{ erg}}{\text{ sec}}) \times (3 \times 10^{10} \frac{\text{ cm}}{\text{ sec}})\times (60 \text{ sec})}{6 \times 10^{-5} \text{cm}}\\
P_{eye} &\approx 2 \times 10^{-9} \frac{ \text{ ergs}}{\text{ sec}}
\end{align}
Now that we know how much power the eye is inputting, we can set up a proportion to compare the surface area of the eye, $SA_{eye}$ and the surface area of the $SA_{supernova}$ with the power input of the eye, $P_{eye}$, with the power output of the supernova, $P_{supernova}$. The proportion is as follows:
\begin{align}
\frac{P_{supernova}}{SA_{supernova}} &= \frac{P_{eye}}{SA_{eye}}\\
\frac{P_{supernova}}{4\pi D^2} &= \frac{P_{eye}}{4\pi R_{eye}^2}
\end{align}
Having this proportionality, we can rearrange the equation above to solve for the distance to the supernova. Assume that the radius of the eye is about 1 cm.
\begin{align}
\frac{P_{supernova}}{4\pi D^2} &= \frac{P_{eye}}{4\pi R_{eye}^2}\\
D &= \left(\frac{R_{eye}^2 \times P_{supernova}}{4 P_{eye}}\right)^{\frac{1}{2}}\\
D &= \left(\frac{(1 \text{ cm})^2 \times (10^{42} \frac{\text{ ergs}}{\text{ second}})}{4 \times (2 \times 10^{-9} \frac{ \text{ ergs}}{\text{ sec}})}\right)^{\frac{1}{2}}\\
D &= 1.12 \times 10^{25} \text{ cm}
\end{align}
Therefore, the supernova exploded $1.12 \times 10^{25} \text{ cm}$ away!!!
Blog #4: Milky Way Rotation
3) You observe a star and you measure its flux to be $F_*$ and it's luminosity to be $L_*$
a) Give an expression for how far away the star is.
The equation that relates a star's flux, luminosity, and distance is given by the equation:
\begin{align}
F_* = \frac{L_*}{4\pi D^2}
\end{align}
In order to figure out how far away the star is, we can rearrange the equation to solve for the radius, $D$, which would be the distance the star is from the observer.
\begin{align}
D = \left(\frac{L_*}{F_* 4 \pi}\right)^{\frac{1}{2}}
\end{align}
b) What is its parallax?
The relationship between the parallax angle, $\theta$, and the distance between a planet and the observed star, $D$, is given by the equation:
\begin{align}
\theta = \frac{1 \text{ AU}}{D}
\end{align}
Since we solved the for the distance of the star in the previous part, we can substitute that distance for $D$ to solve for the parallax angle, $\theta$.
\begin{align}
\theta &= \frac{1 \text{ AU}}{D}\\
\theta &= \frac{1\text{ AU}}{\left(\frac{L_*}{F_* 4 \pi}\right)^{\frac{1}{2}}}\\
\theta &= 1\text{ AU}\left( \frac{F_* 4 \pi}{L_*}\right)^{\frac{1}{2}}
\end{align}
c) If the peak wavelength of its emission is at $\lambda_0$, what is the star's temperature?
A star's temperature, $T$ and maximum wavelength, $\lambda_{max}$ are related by Wien's Displacement Law by a factor, $b = 2.9 \times 10^{-3}$ m K as follows:
\begin{align}
\lambda_{max} = \frac{b}{T}
\end{align}
Since the peak wavelength is $\lambda_{0}$, we can rearranging the previous equation and substitute $\lambda_{max} = \lambda_{0}$ to solve for the temperature as follows:
\begin{align}
T = \frac{b}{\lambda_0}
\end{align}
d) What is the star's radius, $R_*$?
We can use the relationship between the star's temperature and its radius using the equation for luminosity:
\begin{align}
L_* = 4\pi R_*^2 \sigma T_*^4
\end{align}
Rearranging this equation to solve for the radius, $R_*$, we get:
\begin{align}
R_* = \left(\frac{L_*}{4 \pi \sigma T_*^4}\right)^{\frac{1}{2}}\\
\end{align}
Finally, we can substitute $T_*$ with the expression for temperature we got in part c to get the radius, $R_*$, as follows:
\begin{align}
R_* &= \left(\frac{L_*}{4 \pi \sigma \left(\frac{b}{\lambda_0}\right)^4}\right)^{\frac{1}{2}}\\
R_* &= \left(\frac{L_* \lambda_0^4}{4 \pi \sigma b^4}\right)^{\frac{1}{2}}\\
\end{align}
a) Give an expression for how far away the star is.
The equation that relates a star's flux, luminosity, and distance is given by the equation:
\begin{align}
F_* = \frac{L_*}{4\pi D^2}
\end{align}
In order to figure out how far away the star is, we can rearrange the equation to solve for the radius, $D$, which would be the distance the star is from the observer.
\begin{align}
D = \left(\frac{L_*}{F_* 4 \pi}\right)^{\frac{1}{2}}
\end{align}
b) What is its parallax?
The relationship between the parallax angle, $\theta$, and the distance between a planet and the observed star, $D$, is given by the equation:
\begin{align}
\theta = \frac{1 \text{ AU}}{D}
\end{align}
Since we solved the for the distance of the star in the previous part, we can substitute that distance for $D$ to solve for the parallax angle, $\theta$.
\begin{align}
\theta &= \frac{1 \text{ AU}}{D}\\
\theta &= \frac{1\text{ AU}}{\left(\frac{L_*}{F_* 4 \pi}\right)^{\frac{1}{2}}}\\
\theta &= 1\text{ AU}\left( \frac{F_* 4 \pi}{L_*}\right)^{\frac{1}{2}}
\end{align}
c) If the peak wavelength of its emission is at $\lambda_0$, what is the star's temperature?
A star's temperature, $T$ and maximum wavelength, $\lambda_{max}$ are related by Wien's Displacement Law by a factor, $b = 2.9 \times 10^{-3}$ m K as follows:
\begin{align}
\lambda_{max} = \frac{b}{T}
\end{align}
Since the peak wavelength is $\lambda_{0}$, we can rearranging the previous equation and substitute $\lambda_{max} = \lambda_{0}$ to solve for the temperature as follows:
\begin{align}
T = \frac{b}{\lambda_0}
\end{align}
d) What is the star's radius, $R_*$?
We can use the relationship between the star's temperature and its radius using the equation for luminosity:
\begin{align}
L_* = 4\pi R_*^2 \sigma T_*^4
\end{align}
Rearranging this equation to solve for the radius, $R_*$, we get:
\begin{align}
R_* = \left(\frac{L_*}{4 \pi \sigma T_*^4}\right)^{\frac{1}{2}}\\
\end{align}
Finally, we can substitute $T_*$ with the expression for temperature we got in part c to get the radius, $R_*$, as follows:
\begin{align}
R_* &= \left(\frac{L_*}{4 \pi \sigma \left(\frac{b}{\lambda_0}\right)^4}\right)^{\frac{1}{2}}\\
R_* &= \left(\frac{L_* \lambda_0^4}{4 \pi \sigma b^4}\right)^{\frac{1}{2}}\\
\end{align}
Blog #3: Drawing our Galaxy
Create an illustration of the Milky Way galaxy as viewed from outside the galaxy, viewed from the side, and from above. The things to point out are:
a) Location of the Sun
b) Thin/Thick disks, bulge, halo
c) Globular clusters
d) The Small Magellanic Cloud (SMC) and the Large Magellanic Cloud (LMC)
e) Sgr A* (Black hole)
f) Location of Orion star forming region, and the nearest and furthest (known) open clusters to the Sun
g) Scale length and scale height (in order to draw galaxy to scale)
Top View:
Side View:
a) Location of the Sun
b) Thin/Thick disks, bulge, halo
c) Globular clusters
d) The Small Magellanic Cloud (SMC) and the Large Magellanic Cloud (LMC)
e) Sgr A* (Black hole)
f) Location of Orion star forming region, and the nearest and furthest (known) open clusters to the Sun
g) Scale length and scale height (in order to draw galaxy to scale)
Top View:
Side View:
Blog #2: Milkomeda
2) How long will it take for Andromeda to collide with the Milky Way? The time-scale here is the free-fall time, $t_{ff}$. A way of finding this is to assume that Andromeda is on a highly elliptical orbit $(e \rightarrow 1)$ around the Milky Way. With this assumption, we can use Kepler's Third Law:
\begin{align}
P^2 = \frac{4\pi^2 a^3}{G(M_{MW} + M_{And})}
\end{align}
where $P$ is the period of the orbit and $a$ is the semi-major axis. How does $t_ff$ relate to the period? Estimate it to an order of magnitude.
Assuming that Andromeda is on a highly elliptical orbit around the Milky Way since the eccentricity is approaching 1 $(e \rightarrow 1)$, it is approximately a straight line free fall between Andromeda and the Milky Way. We can use the Milky Way as a fixed point on one side of the ellipse because that is our frame of reference. We can use Andromeda on the opposite end of the ellipse because we want to model the free-fall effects of Andromeda onto the Milky Way. It is useful to know that Andromeda is 800 kpc away from the Milky Way. Some other useful values to know are:
\begin{align}
a = 800\text{ kpc} = 2.5 \times 10^{24} \text{ cm}\\
G = 6.67 \times 10^{-8} \frac{cm^3}{g \cdot s^2}\\
M_{MW} + M_{And} = 2 \times 10^{45} g
\end{align}
Using Kepler's Third Law, we know that an an object orbits another object in time $P$. Since Andromeda is half-way through it's highly elliptical orbit, the free fall time, $t_{ff} = \frac{1}{2} P$. In order to find the $t_{ff}$, we can use Kepler's Third Law to solve for $P$.
\begin{align}
t_{ff} &= \frac{1}{2} P\\
t_{ff} &= \frac{1}{2} \left( \frac{4\pi^2 a^3}{G(M_{MW} + M_{And})} \right)^{\frac{1}{2}}\\
t_{ff} &= \frac{1}{2} \left( \frac{4\pi^2 (2.5 \times 10^{24} \text{ cm})^3}{6.67 \times 10^{-8} \frac{cm^3}{g \cdot s^2}(2 \times 10^{45}\text{ g})} \right)^{\frac{1}{2}}\\
t_{ff} &= 1.06 \times 10^{18} \text{ seconds}
\end{align}
The free fall time of the in which Andromeda will collide with the Milky Way is $1.06 \times 10^{18}$ seconds, which is $3 \times 10^{10}$ years!
3) Let's estimate the average number density of stars throughout the Milky Way, $n$. First, we need to clarify the distribution of stars. Stars are concentrated in the center of the galaxy, and their density decreases exponentially:
\begin{align}
n(r) \propto exp(-\frac{r}{R_s})
\end{align}
$R_s$ is also known as the "scale radius" of the galaxy. The Milky Way has a scale radius of 3.5 kpc. With that in mind, estimate $n$ in two ways:
\begin{align}
P^2 = \frac{4\pi^2 a^3}{G(M_{MW} + M_{And})}
\end{align}
where $P$ is the period of the orbit and $a$ is the semi-major axis. How does $t_ff$ relate to the period? Estimate it to an order of magnitude.
Assuming that Andromeda is on a highly elliptical orbit around the Milky Way since the eccentricity is approaching 1 $(e \rightarrow 1)$, it is approximately a straight line free fall between Andromeda and the Milky Way. We can use the Milky Way as a fixed point on one side of the ellipse because that is our frame of reference. We can use Andromeda on the opposite end of the ellipse because we want to model the free-fall effects of Andromeda onto the Milky Way. It is useful to know that Andromeda is 800 kpc away from the Milky Way. Some other useful values to know are:
\begin{align}
a = 800\text{ kpc} = 2.5 \times 10^{24} \text{ cm}\\
G = 6.67 \times 10^{-8} \frac{cm^3}{g \cdot s^2}\\
M_{MW} + M_{And} = 2 \times 10^{45} g
\end{align}
Using Kepler's Third Law, we know that an an object orbits another object in time $P$. Since Andromeda is half-way through it's highly elliptical orbit, the free fall time, $t_{ff} = \frac{1}{2} P$. In order to find the $t_{ff}$, we can use Kepler's Third Law to solve for $P$.
\begin{align}
t_{ff} &= \frac{1}{2} P\\
t_{ff} &= \frac{1}{2} \left( \frac{4\pi^2 a^3}{G(M_{MW} + M_{And})} \right)^{\frac{1}{2}}\\
t_{ff} &= \frac{1}{2} \left( \frac{4\pi^2 (2.5 \times 10^{24} \text{ cm})^3}{6.67 \times 10^{-8} \frac{cm^3}{g \cdot s^2}(2 \times 10^{45}\text{ g})} \right)^{\frac{1}{2}}\\
t_{ff} &= 1.06 \times 10^{18} \text{ seconds}
\end{align}
The free fall time of the in which Andromeda will collide with the Milky Way is $1.06 \times 10^{18}$ seconds, which is $3 \times 10^{10}$ years!
3) Let's estimate the average number density of stars throughout the Milky Way, $n$. First, we need to clarify the distribution of stars. Stars are concentrated in the center of the galaxy, and their density decreases exponentially:
\begin{align}
n(r) \propto exp(-\frac{r}{R_s})
\end{align}
$R_s$ is also known as the "scale radius" of the galaxy. The Milky Way has a scale radius of 3.5 kpc. With that in mind, estimate $n$ in two ways:
- Consider that within a 2 pc radius of the Sun there are five stars: the Sun, $\alpha$ Centauri A and B, Proxima Centauri, and Barnard's Star.
- The Galaxy's "scale height" is 330 pc. Use the galaxy's scale lengths as the lengths of the volume within the Galaxy containing most of the stars. Assume a typical stellar mass of $0.5M_{\odot}$.
Let's consider the first case, where the frame of reference is the Sun, with 4 other stars within 2 pc:
Given the equation $n(r) \propto exp(-\frac{r}{R_s})$, where $n(r)$ is the number density ($ n = \frac{\text{# of items}}{\text{volume items occupy}}$) of the number of stars as a function of radius, $r$, and $R_s$ as the scale radius of the galaxy, we can solve for the number density at the center of the galaxy, $n_0$.
But wait, we need more information! Even if we are using the Sun as a frame of reference to other stars, we still need to know how far the Sun is away from the galactic center, $r$. A quick Google search will tell us that the Sun is about 8 kpc away from the galactic center, so $r = 8 kpc$ We also know that the scale radius of the Milky Way is $R_s = 3.5$. Using this information, we can calculate the number density of stars at the galactic center.
But wait, we need more information! Even if we are using the Sun as a frame of reference to other stars, we still need to know how far the Sun is away from the galactic center, $r$. A quick Google search will tell us that the Sun is about 8 kpc away from the galactic center, so $r = 8 kpc$ We also know that the scale radius of the Milky Way is $R_s = 3.5$. Using this information, we can calculate the number density of stars at the galactic center.
\begin{align}
n &= n_0 e^{-\frac{r}{R_s}} \\
n_0 &= n e^{\frac{r}{R_s}}\\
n_0 &= \frac{\text{# of stars}}{\text{volume stars occupy}}e^{\frac{r}{R_s}}\\
n_0 &= \frac{5 \text{ stars}}{\frac{4}{3}\pi \cdot (2 \text{pc})^3}e^{\frac{8 \text{ kpc}}{3.5\text{ kpc}}}\\
n_0 &\approx 1.5 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
Therefore, using the Sun as a frame of reference, we know that the number density at the center of the galaxy is $n_0 = 1.5$ stars for every cubic parsec.
In this model, we assumed that the majority of stars are located in the center of the galaxy, which is why we can assume that the number density at the center, $n_0$ is the highest, and decreases exponentially the further away from the center you go. So, for example, knowing that the Milky Way Galaxy has a radius, $r = 15$ kpc, we can use the number density function, $n(r)$ to solve for the number density over the entire galaxy:
\begin{align}
n(r) &= n_0 e^{-\frac{r}{R_s}} \\
n(15) &= 1.5 \frac{\text{ stars}}{\text{ pc}^3} e^{-\frac{15}{3.5}}\\
n(15) &\approx 0.02 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
This shows that the number density of stars over the entire galaxy is very small, with about 0.02 stars for every cubic parsec
Let's consider the other situation of finding the galactic number density using the "scale height". In order to use the "scale height", we can visualize the Milky Way as a cylindrical shape as follows:
How many stars will collide every year? Is the Sun safe, or likely to collide with another star?
In order to figure out the collision rate of stars, $K_{collision}$, we can use the number density, $n = 0.03 \frac{\text{ stars}}{\text{ pc}^3}$, the cross-sectional area of a star, such as the Sun, which is $\sigma_{*}$, and the average velocity of Milkomeda's stars, $\overline{v}$. The relationship between $K_{collision}, n, \sigma_{*}$ and $\overline{v}$ can be modeled by the equation:
\begin{align}
K_{collision} = n \times \sigma_{*} \times \overline{v}
\end{align}
$ \sigma_{*}$ is the cross-sectional area of a star, which can be calculated using $A = \pi R_{\odot}^2$. We know that the radius of of the Sun is$R_{\odot} = 6.96 \times 10^{10}$, so we can calculate $\sigma_{*}$ as follows:
\begin{align}
\sigma_* &= \pi R_{\odot}^2\\
\sigma_* &= \pi (6.96 \times 10^{10})^2\\
\sigma_* &= 1.52 \times 10^{22} \text{ cm}^2
\end{align}
We can also calculate the average velocity of stars as they collide using $\overline{v} = \frac{\text{distance}}{\text{time}}$, where the distance between the Milky Way and Andromeda is $800 \text{ kpc} = 2.5 \times 10^{24} \text{ cm}$, and the time to the collision is $t_{ff}$ calculated earlier.
\begin{align}
\overline{v} &= \frac{\text{distance}}{\text{time}}\\
\overline{v} &= \frac{2.5 \times 10^{24} \text{ cm}}{1.06 \times 10^{18} \text{ seconds}}\\
\overline{v} &= 2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}}
\end{align}
Now that we know both $\overline{v}$ and $\sigma_*$, we can calculate $K_{collisions}$ as follows:
\begin{align}
K_{collision} &= n \times \sigma_{*} \times \overline{v}\\
K_{collision} &= (0.03 \frac{\text{ stars}}{\text{ pc}^3}) \times (1.52 \times 10^{22} \text{ cm}^2) \times (2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}})\\
K_{collision} &= (1.01 \times 10^{-57 } \frac{\text{ stars}}{\text{ cm}^3}) \times (1.52 \times 10^{22} \text{ cm}^2) \times (2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}})\\
K_{collision} &= 3.7 \times 10^{-29}\frac{\text{ stars}}{\text{ second}}
\end{align}
This shows that during the collision of Milkomeda, the chance of stars colliding is on the scale of $3.7 \times 10^{-29}\frac{\text{ stars}}{\text{ second}}$, or $1.17 \times 10^{-21}$ collisions per year!!! That is effectively zero, so the chances of the Sun colliding with another star are close to 0.
n &= n_0 e^{-\frac{r}{R_s}} \\
n_0 &= n e^{\frac{r}{R_s}}\\
n_0 &= \frac{\text{# of stars}}{\text{volume stars occupy}}e^{\frac{r}{R_s}}\\
n_0 &= \frac{5 \text{ stars}}{\frac{4}{3}\pi \cdot (2 \text{pc})^3}e^{\frac{8 \text{ kpc}}{3.5\text{ kpc}}}\\
n_0 &\approx 1.5 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
Therefore, using the Sun as a frame of reference, we know that the number density at the center of the galaxy is $n_0 = 1.5$ stars for every cubic parsec.
In this model, we assumed that the majority of stars are located in the center of the galaxy, which is why we can assume that the number density at the center, $n_0$ is the highest, and decreases exponentially the further away from the center you go. So, for example, knowing that the Milky Way Galaxy has a radius, $r = 15$ kpc, we can use the number density function, $n(r)$ to solve for the number density over the entire galaxy:
\begin{align}
n(r) &= n_0 e^{-\frac{r}{R_s}} \\
n(15) &= 1.5 \frac{\text{ stars}}{\text{ pc}^3} e^{-\frac{15}{3.5}}\\
n(15) &\approx 0.02 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
This shows that the number density of stars over the entire galaxy is very small, with about 0.02 stars for every cubic parsec
Let's consider the other situation of finding the galactic number density using the "scale height". In order to use the "scale height", we can visualize the Milky Way as a cylindrical shape as follows:
In this case, the majority of the stars are in this cylinder. We can use the equation we derived in the first part to get the number density of stars in this cylinder using the equation for a volume of a cylinder, $V = \pi r^2 h$. In this case, the height of the cylinder, $h$ can be represented by the scale height of the galaxy, $h = H_s$, and the radius of the cylinder, $r$ can be represented by the scale radius, $r = R_s$. Also, the number of stars in the entire galaxy can be obtained by using the total mass of the Milky Way, $M_{MW} = 10^{10} M_{\odot}$ and the mass of the average star in the Milky Way, $M_* = 0.5 M_{\odot}$. Finally, since we are using the cylindar as the boundary for stars, the radius, $r = R_s$. Using this information, we can get the number density of stars in the center of this cylindrical galaxy as follows:
\begin{align}
n_0 &= n e^{\frac{r}{R_s}}\\
n_0 &= \frac{\text{# of stars}}{\text{volume stars occupy}}e^{\frac{r}{R_s}}\\
n_0 &= \frac{\frac{M_{MW}}{M_*}}{\pi R_s^2 H_s}e^{\frac{R_s}{R_s}}\\
n_0 &= \frac{\frac{10^{10} M_{\odot}}{0.5 M_{\odot}}}{\pi (3500 \text{ pc})^2 (330 \text{ pc})}e\\
n_0 &= \frac{2 \times 10^{10} \text{ stars}}{1.3 \times 10^{10}\text{ pc}^3}e\\
n_0 &\approx 4.3 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
Based on the above calculation, the number density of the stars in this cylinder of scale radius 3500 pc of the galaxy is about 4.3 stars per cubic parsec.
In order to determine the number density of stars over the entire galaxy, we can use the number density function, $n(r)$ to calculate the number density of the Milky Way over its entire radius, $r = 15 kpc$ as follows:
\begin{align}
n(r) &= n_0 e^{-\frac{r}{R_s}} \\
n(15) &= 4.3 \frac{\text{ stars}}{\text{ pc}^3} e^{-\frac{15}{3.5}}\\
n(15) &\approx 0.03 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
This cylindrical model shows that at over the entire galaxy, the number density of stars is 0.03 stars per cubic parsec.
4) Determine the collision collision rate of the stars using the number density of the stars ($n$), the cross-section for a star $\sigma_{*}$, and the average velocity of Milkomeda's stars as they collide $\overline{v}$.\begin{align}
n_0 &= n e^{\frac{r}{R_s}}\\
n_0 &= \frac{\text{# of stars}}{\text{volume stars occupy}}e^{\frac{r}{R_s}}\\
n_0 &= \frac{\frac{M_{MW}}{M_*}}{\pi R_s^2 H_s}e^{\frac{R_s}{R_s}}\\
n_0 &= \frac{\frac{10^{10} M_{\odot}}{0.5 M_{\odot}}}{\pi (3500 \text{ pc})^2 (330 \text{ pc})}e\\
n_0 &= \frac{2 \times 10^{10} \text{ stars}}{1.3 \times 10^{10}\text{ pc}^3}e\\
n_0 &\approx 4.3 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
Based on the above calculation, the number density of the stars in this cylinder of scale radius 3500 pc of the galaxy is about 4.3 stars per cubic parsec.
In order to determine the number density of stars over the entire galaxy, we can use the number density function, $n(r)$ to calculate the number density of the Milky Way over its entire radius, $r = 15 kpc$ as follows:
\begin{align}
n(r) &= n_0 e^{-\frac{r}{R_s}} \\
n(15) &= 4.3 \frac{\text{ stars}}{\text{ pc}^3} e^{-\frac{15}{3.5}}\\
n(15) &\approx 0.03 \frac{\text{ stars}}{\text{ pc}^3}
\end{align}
This cylindrical model shows that at over the entire galaxy, the number density of stars is 0.03 stars per cubic parsec.
How many stars will collide every year? Is the Sun safe, or likely to collide with another star?
In order to figure out the collision rate of stars, $K_{collision}$, we can use the number density, $n = 0.03 \frac{\text{ stars}}{\text{ pc}^3}$, the cross-sectional area of a star, such as the Sun, which is $\sigma_{*}$, and the average velocity of Milkomeda's stars, $\overline{v}$. The relationship between $K_{collision}, n, \sigma_{*}$ and $\overline{v}$ can be modeled by the equation:
\begin{align}
K_{collision} = n \times \sigma_{*} \times \overline{v}
\end{align}
$ \sigma_{*}$ is the cross-sectional area of a star, which can be calculated using $A = \pi R_{\odot}^2$. We know that the radius of of the Sun is$R_{\odot} = 6.96 \times 10^{10}$, so we can calculate $\sigma_{*}$ as follows:
\begin{align}
\sigma_* &= \pi R_{\odot}^2\\
\sigma_* &= \pi (6.96 \times 10^{10})^2\\
\sigma_* &= 1.52 \times 10^{22} \text{ cm}^2
\end{align}
We can also calculate the average velocity of stars as they collide using $\overline{v} = \frac{\text{distance}}{\text{time}}$, where the distance between the Milky Way and Andromeda is $800 \text{ kpc} = 2.5 \times 10^{24} \text{ cm}$, and the time to the collision is $t_{ff}$ calculated earlier.
\begin{align}
\overline{v} &= \frac{\text{distance}}{\text{time}}\\
\overline{v} &= \frac{2.5 \times 10^{24} \text{ cm}}{1.06 \times 10^{18} \text{ seconds}}\\
\overline{v} &= 2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}}
\end{align}
Now that we know both $\overline{v}$ and $\sigma_*$, we can calculate $K_{collisions}$ as follows:
\begin{align}
K_{collision} &= n \times \sigma_{*} \times \overline{v}\\
K_{collision} &= (0.03 \frac{\text{ stars}}{\text{ pc}^3}) \times (1.52 \times 10^{22} \text{ cm}^2) \times (2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}})\\
K_{collision} &= (1.01 \times 10^{-57 } \frac{\text{ stars}}{\text{ cm}^3}) \times (1.52 \times 10^{22} \text{ cm}^2) \times (2.36 \times 10^{6} \frac{\text{ cm}}{\text{ seconds}})\\
K_{collision} &= 3.7 \times 10^{-29}\frac{\text{ stars}}{\text{ second}}
\end{align}
This shows that during the collision of Milkomeda, the chance of stars colliding is on the scale of $3.7 \times 10^{-29}\frac{\text{ stars}}{\text{ second}}$, or $1.17 \times 10^{-21}$ collisions per year!!! That is effectively zero, so the chances of the Sun colliding with another star are close to 0.
Blog #1: Hello Universe, Round 2!
Hey everyone!
For those of you who know me, hello again! I'm so excited for round 2 of this astronomy adventure.
For those of you who don't know me, my name is Zahra Mahmood, and I am a senior at Harvard University in Quincy House concentrating in Computer Science. I am also pursuing a secondary in Astrophysics.
I became interested in Astronomy when I was about 5 years old. I absorbed all the documentaries about planetary and cosmological journeys, and wanted to be a part of the experience of increase our knowledge about the universe.
Based on my experience in Astronomy 16, I am firmly committed to doing a secondary in Astrophysics, and potentially even find a future career in the field. As a senior who is in the process of job hunting, I am applying to SpaceX to work as a software engineer. As a CS concentrator, I want to intertwine my love for astronomy with my practical skills as programmer to do work for companies at the frontier of space exploration.
Therefore, I am super excited about this upcoming semester, and look forward to all the cool stuff we'll be leaning.
For those of you who know me, hello again! I'm so excited for round 2 of this astronomy adventure.
For those of you who don't know me, my name is Zahra Mahmood, and I am a senior at Harvard University in Quincy House concentrating in Computer Science. I am also pursuing a secondary in Astrophysics.
I became interested in Astronomy when I was about 5 years old. I absorbed all the documentaries about planetary and cosmological journeys, and wanted to be a part of the experience of increase our knowledge about the universe.
Based on my experience in Astronomy 16, I am firmly committed to doing a secondary in Astrophysics, and potentially even find a future career in the field. As a senior who is in the process of job hunting, I am applying to SpaceX to work as a software engineer. As a CS concentrator, I want to intertwine my love for astronomy with my practical skills as programmer to do work for companies at the frontier of space exploration.
Therefore, I am super excited about this upcoming semester, and look forward to all the cool stuff we'll be leaning.
Thursday, May 14, 2015
Day Lab (Part 4): The Astronomical Unit
Okay, so in the last 3 parts of this lab, we calculated the following values:
But what we actually want to calculate is the astronomical unit (AU). How can we find it though?
Well, let's draw a diagram that relates the astronomical unit to the angular diameter:
Based on this diagram, we can relate the astronomical unit to the angular diameter of the Sun, $\theta_{\odot}$ and the radius of the Sun, $R_{\odot}$:
\begin{align}
\tan \left(\frac{\theta_{\odot}}{2}\right) &= \frac{R_{\odot}}{AU}\\
AU &= \frac{R_{\odot}}{\tan \left(\frac{\theta_{\odot}}{2}\right)}
\end{align}
Okay, so we have an equation for calculating AU, but it requires us to have the radius of the Sun, $R_{\odot}$. We don't have that value, but we can calculate it using the Sun's rotational speed, $v_{\odot}$ and the rotational period, $P_{\odot}$ using the equation for rotational velocity:
\begin{align}
v_{\odot} &= \frac{2\pi R_{\odot}}{P_{\odot}}\\
R_{\odot} &= \frac{v_{\odot} \times P_{\odot}}{2\pi}\\
R_{\odot} &= \frac{1.86 \frac{km}{s} \cdot \frac{10^5 \text{ cm}}{1 \text{ km}}\times 26.1 \text{ days} \cdot \frac{24 \text{ hours}}{1 \text{ day}} \cdot \frac{60 \text{ minutes}}{1 \text{ hour}} \cdot \frac{60 \text{ seconds}}{1 \text{ minute}}}{2\pi}\\
R_{\odot} &= 6.68 \times 10^{10} \text{ cm}
\end{align}
Now that we have the radius of the Sun, we can plug this value into the first equation to solve for the AU:
\begin{align}
AU &= \frac{R_{\odot}}{\tan \left(\frac{\theta_{\odot}}{2}\right)}\\
AU &= \frac{6.68 \times 10^{10} \text{ cm}}{\tan \left(\frac{0.5547°}{2}\right)}\\
AU &= 1.379 \times 10^{13} \text{ cm}
\end{align}
We have calculated the AU to be $1.379 \times 10^{13} \text{ cm}$, which is very close to the actual answer of $1.5 \times 10^{13} \text{ cm}$, which is within 8% error. This can be due to the inaccuracies in measuring the sunspot latitudes, since the spherical grid was not very precise since it lacked small unit divisions. Also, measuring the angular diameter could be inaccurate due to human error of stopping the stopwatch at the accurate time.
- Angular diameter of the Sun, $\theta_{\odot} = 0.5547°$
- Rotational speed of the Sun, $v_{\odot} = 1.86 \frac{km}{s}$
- Rotational period of the Sun, $P_{\odot} = 26.1$ days
But what we actually want to calculate is the astronomical unit (AU). How can we find it though?
Well, let's draw a diagram that relates the astronomical unit to the angular diameter:
Based on this diagram, we can relate the astronomical unit to the angular diameter of the Sun, $\theta_{\odot}$ and the radius of the Sun, $R_{\odot}$:
\begin{align}
\tan \left(\frac{\theta_{\odot}}{2}\right) &= \frac{R_{\odot}}{AU}\\
AU &= \frac{R_{\odot}}{\tan \left(\frac{\theta_{\odot}}{2}\right)}
\end{align}
Okay, so we have an equation for calculating AU, but it requires us to have the radius of the Sun, $R_{\odot}$. We don't have that value, but we can calculate it using the Sun's rotational speed, $v_{\odot}$ and the rotational period, $P_{\odot}$ using the equation for rotational velocity:
\begin{align}
v_{\odot} &= \frac{2\pi R_{\odot}}{P_{\odot}}\\
R_{\odot} &= \frac{v_{\odot} \times P_{\odot}}{2\pi}\\
R_{\odot} &= \frac{1.86 \frac{km}{s} \cdot \frac{10^5 \text{ cm}}{1 \text{ km}}\times 26.1 \text{ days} \cdot \frac{24 \text{ hours}}{1 \text{ day}} \cdot \frac{60 \text{ minutes}}{1 \text{ hour}} \cdot \frac{60 \text{ seconds}}{1 \text{ minute}}}{2\pi}\\
R_{\odot} &= 6.68 \times 10^{10} \text{ cm}
\end{align}
Now that we have the radius of the Sun, we can plug this value into the first equation to solve for the AU:
\begin{align}
AU &= \frac{R_{\odot}}{\tan \left(\frac{\theta_{\odot}}{2}\right)}\\
AU &= \frac{6.68 \times 10^{10} \text{ cm}}{\tan \left(\frac{0.5547°}{2}\right)}\\
AU &= 1.379 \times 10^{13} \text{ cm}
\end{align}
We have calculated the AU to be $1.379 \times 10^{13} \text{ cm}$, which is very close to the actual answer of $1.5 \times 10^{13} \text{ cm}$, which is within 8% error. This can be due to the inaccuracies in measuring the sunspot latitudes, since the spherical grid was not very precise since it lacked small unit divisions. Also, measuring the angular diameter could be inaccurate due to human error of stopping the stopwatch at the accurate time.
Day Lab (Part 3): Rotational Period of the Sun
In the first two parts of the lab, we calculated the angular diameter of the Sun, $\theta_{\odot} = 0.5547°$ and the rotational velocity of the Sun, $v_{\odot} = 1.86 km/s$. Using these two values, we can calculate the time it takes for the Sun to make one full rotation, also known as it's period, $P_{\odot}$.
In order to calculate the full rotation of the Sun, it would make sense to use a marker on the Sun, and see how long it takes to see that marker again, which would indicate the period, $P_{\odot}$. Unfortunately, there are no permanent markers on the Sun, since the surface of the Sun is constantly changing. However, we do have temporary markers on the Sun, sunspots, which can be tracked as the Sun is rotating. Using sunspots, we can create a relationship between the the angular distance, $\theta$ a sunspot travels as it moves across the surface of the Sun over a given period of time, $t$, and the rotational period of the Sun, $P_{\odot}$ as it travels a full 360°.
This relationship can be modeled as follows:
\begin{align}
\frac{P_{\odot}}{360°} &= \frac{\Delta t}{\Delta \theta}\\
P_{\odot} &= \frac{\Delta t (360°)}{\Delta \theta}
\end{align}
Okay, so we have a model to calculate the period, but how do we measure the transit of the sunspots across the surface of the Sun?
Well, we could directly view sunspots by projecting an image of the Sun via mirrors on a piece of paper, and see how the sunspots that are visible over the course of a few days. However, when doing this lab, the day was rather cloudy, so we decided to use sunspot data from NASA in 2001.
Using this data, we can overlay a live recording of the surface of the Sun with graph of spherical coordinates, and measure the change in angular distance over a given period of time. In this lab, we recorded the transit of 3 sunspots, with the following data:
Having three measurements of rotational period, $P_{\odot}$, we can take the average of all three to get the rotational period of the Sun to be $P_{\odot} = 26.1$ days. The actual rotational period of the Sun at the equator is 24.7 days, but that is the sidereal rotation period. The method we used to get the period required following a fixed feature on the Sun, which is measured by synodic rotational period, which for the Sun is 26.24 days. The synodic rotational period of the Sun is very close to our measurements.
In order to calculate the full rotation of the Sun, it would make sense to use a marker on the Sun, and see how long it takes to see that marker again, which would indicate the period, $P_{\odot}$. Unfortunately, there are no permanent markers on the Sun, since the surface of the Sun is constantly changing. However, we do have temporary markers on the Sun, sunspots, which can be tracked as the Sun is rotating. Using sunspots, we can create a relationship between the the angular distance, $\theta$ a sunspot travels as it moves across the surface of the Sun over a given period of time, $t$, and the rotational period of the Sun, $P_{\odot}$ as it travels a full 360°.
This relationship can be modeled as follows:
\begin{align}
\frac{P_{\odot}}{360°} &= \frac{\Delta t}{\Delta \theta}\\
P_{\odot} &= \frac{\Delta t (360°)}{\Delta \theta}
\end{align}
Okay, so we have a model to calculate the period, but how do we measure the transit of the sunspots across the surface of the Sun?
Well, we could directly view sunspots by projecting an image of the Sun via mirrors on a piece of paper, and see how the sunspots that are visible over the course of a few days. However, when doing this lab, the day was rather cloudy, so we decided to use sunspot data from NASA in 2001.
Using this data, we can overlay a live recording of the surface of the Sun with graph of spherical coordinates, and measure the change in angular distance over a given period of time. In this lab, we recorded the transit of 3 sunspots, with the following data:
Sunspot 1:
Trial 1: 03-04-2001 at 17:36 to 03-09-2001 at 11:12
$\Delta \theta = +70°$, $\Delta t = 408,960$ seconds
Trial 2: 03-06-2001 at 00:00 to 03-08-2001 at 17:36
$\Delta \theta = +40°$, $\Delta t = 236,160$ seconds
Trial 3: 03-05-2001 at 11:12 to 03-10-2001 at 00:00
$\Delta \theta = +67°$, $\Delta t = 291,680$ seconds
Average:
$\Delta \theta = 59°$, $\Delta t = 345,600$ seconds
$P_{\odot} = \frac{\Delta t (360°)}{\Delta \theta} = \frac{345,600 (360°)}{59°} =$ 24.4 days
Sunspot 2:
Trial 1: 03-22-2001 at 00:00 to 03-25-2001 at 11:12
$\Delta \theta = +50°$, $\Delta t = 299,520$ seconds
Trial 2: 03-20-2001 at 17:36 to 03-27-2001 at 17:36
$\Delta \theta = +100°$, $\Delta t = 604,800$ seconds
Trial 3: 03-22-2001 at 17:36 to 03-27-2001 at 00:14
$\Delta \theta = +60°$, $\Delta t = 369,480$ seconds
Average:
$\Delta \theta = 70°$, $\Delta t = 424,600$ seconds
$P_{\odot} = \frac{\Delta t (360°)}{\Delta \theta} = \frac{424,600 (360°)}{70°} =$ 25.3 days
Sunspot 3:
Trial 1: 04-06-2001 at 08:45 to 04-11-2001 at 00:00
$\Delta \theta = +60°$, $\Delta t = 400,500$ seconds
Trial 2: 04-04-2001 at 19:12 to 04-10-2001 at 06:24
$\Delta \theta = +70°$, $\Delta t = 472,200$ seconds
Trial 3: 04-07-2001 at 00:00 to 04-14-2001 at 11:12
$\Delta \theta = +90°$, $\Delta t = 645,120$ seconds
Average:
$\Delta \theta = 73.3°$, $\Delta t = 505,940$ seconds
$P_{\odot} = \frac{\Delta t (360°)}{\Delta \theta} = \frac{505,940 (360°)}{73.3°} =$ 28.7 days
Having three measurements of rotational period, $P_{\odot}$, we can take the average of all three to get the rotational period of the Sun to be $P_{\odot} = 26.1$ days. The actual rotational period of the Sun at the equator is 24.7 days, but that is the sidereal rotation period. The method we used to get the period required following a fixed feature on the Sun, which is measured by synodic rotational period, which for the Sun is 26.24 days. The synodic rotational period of the Sun is very close to our measurements.
Subscribe to:
Posts (Atom)















