- Convince yourself that the brightness pattern of light on the screen is a cosine function. (HINT: Think about the conditions for constructive and destructive interference of the light waves emerging from each slit).
- Now imagine a second set of slits placed just inwards of the first set. How does the second set of slits modify the brightness pattern on the screen?
- Imagine a continuous set of slit pairs with ever decreasing separation. What is the resulting brightness pattern?
- Notice that this continuous set of slits forms a "top hat" transmission function. What is the Fourier transform of a top hat, and how does this compare to your sum from the previous step?
- For the top hat function's FT, what is the relationship between the distance between the first nulls and the width of the top hat (HINT: it involves the wavelength of light and the width of the aperture)? Express your results as a proportionality in terms of only the wavelength of light $\lambda$ and the diameter of the top hat $D$.
- Take a step back and think about what I am trying to teach you with this activity, and how it relates to a telescope's primary mirror?
WHEW.... that is a long problem, but lets approach it one step at a time to see just what is the significance of a telescope's primary mirror. To start off, just as the problem suggests, lets draw a diagram of the double slit setup.
Now the first part of the problem asks to:
(A) Convince yourself that the brightness pattern of light on the screen is a cosine function.
If you look at Figure 1, you can see that the constructive (pink) and destructive (blue) interference of light. Constructive interference of light is when the crests, or the troughs of two wave are aligned with one another so as to increase the amplitude of the wave. Destructive interference is when the crest of one wave, and the trough of another wave are aligned with one another so as to decrease the amplitude of a wave. In Figure 1, all the constructive interferences (pink) are linearly aligned as to project a constructive wave pattern on the phosphorescent screen. In a similar manner, all the deconstructive interferences (blue) are also linearly aligned, between the line of constructive interferences, to project a deconstructive wave pattern between the constructive wave pattern on the phosphorescent screen. If you create a wave that is the sum of the constructive and destructive interference projected on the phosphorescent screen, you will see a wave is created that reflects the changed amplitudes. Since the pattern on the phosphorescent screen is a result of constructive and deconstructive interference which results in a new wave, and since all waves can be represented as a cosine function, the pattern of light on the screen is a cosine function.
Okay, so that was one way to show, intuitively, by constructive and deconstructive interference, you get a wave, which is represented by a cosine function. However, is there a more rigorous way to prove the relationship between the constructive and deconstructive interference that is actually happening? Yup! Let's start on a blank slate, and look at the distances light has to travel, to get a more mathematical understanding of why the pattern of light is a cosine function.
 |
| Figure 2: The light coming through the two slits converges at a point on the phosphorescent screen. |
From Figure 2, it is apparent that light can converge at any point on the phosphorescent screen (this would only be one of the many places light can converge, but we are using one point for the sake of simplicity). Since light must travel different distances to reach the same point because of the distance $D$ between the two slits, the change in distance, $\Delta l$ represents the difference in distance. Since the point light on the phosphorescent screen is at an angle $\theta$ from the incident light, we can use the distance between the slits $D$ and the difference in distance between the light coming from the two slits, $\Delta l$ to show their relationship to each other using trigonometry.
Based on the relationship between distance in light shown in Figure 3, and the constructive, and destructive interference pattern shown in Figure 1, we can establish the following two relationships:
For constructive interference:
\Delta l = D \cdot \sin \theta = n \lambda\\
\end{align}
For destructive interference:
\begin{align}
\Delta l = D \cdot \sin \theta = \left( \frac{1}{2} + n \right) \lambda\\
\end{align}
This relationship shows that for any crest $n$, such that $n \in \mathbb{Z}$, constructive interference happens when the distance between the length the light has to travel to converge at the phosphorescent screen is an integer multiple of the wavelength of the monochromatic light. For deconstructive interference, the distance between the individual light waves must be a exactly one-half of a wavelength shifted from an integer multiple of the wavelength of monochromatic light. Because the relationship is related through the $\sin$ function, by making $n$ represent the crest, you are essentially shifting the function by $\frac{1}{2} \lambda$, thereby showing that the relationship of light interference in the light pattern on the phosphorescent screen is actually a cosine function!
But wait... that was a lot of work to show that the light pattern on the screen was a cosine function. In fact, there is an easier way to show the same relationship using Fourier transformations! Fo-ri-what-now?!?!
Fourier transformations are linear transformations that allow us to represent other functions as a sum of sines and cosines. Here is a cheat sheet to show how some common functions look like after a Fourier transformation (you'll thank me for this later):
 |
| Figure 4: Fourier transformation cheat sheet! |
Okay, so what does this cheat sheet have to do with proving that the light pattern on the phosphorescent screen creates a cosine function? Well, let's redraw the diagram to look at the which of the common functions provided best represents our double slit experiment:
If you look at the double slit as allowing two beams of light that diffract as they enter the slit, you can see how it resembles the Even Pair function in the Fourier Transformations cheat sheet. And if you look at the Fourier transformation of the Even Pair function, you can see that it turns into a cosine function!
WOWW!!! That was a lot of work to do the first part of the problem. But now that we know how to use Fourier transformation, we'll be able to see other cool connections in how light behaves as a wave.
So as for the second question:
(B) Now imagine a second set of slits placed just inwards of the first set. How does the second set of slits modify the brightness pattern on the screen?
Just like the first problem, let's think about it conceptually before we let the Fourier transformation just give us the answer. Let's look at the diagram for this scenario:
Okay, so we know that we have an outer set of slits separated by distance $D_0$, and an inner set of slits separated by distance $D_1$. Since each set of slits can create its own diffraction pattern, with each slit providing a source of light, there would be more interference, both constructive and destructive. Since the distance $D_0$ is larger than distance $D_1$, the distance between the crests and troughs would be larger, but it would still be a cosine function. Therefore, you are essentially adding 2 cosine functions. Since both of them will have their converging crests be at the point of intersection on the phosphorescent screen, there will be both stronger constructive and destructive interference. Therefore, the brighter spots would be even more brighter, and the darker spots would be even darker.
A visual representation of the constructive and destructive interference is as follows:
Okay, so now we know that we can use Fourier Transformations to add functions together to represent even more complicated functions. That is going to be a very useful strategy for the next concept:
(C) Imagine a continuous set of slit pairs with ever decreasing separation. What is the resulting brightness pattern?
In this case, we are just dealing with an infinite number of slit pairs. Since we will be adding many different cosine functions together, we will have even stronger constructive interference in the center, and very strong destructive interference as you progress outwards from the center. Since only the center will continually have more and more constructive interference, thereby making it much brighter, while the outskirts away from the center will be a mixture of crests and troughs all over the place, the deconstructive interference will make the outer bands much dimmer. Therefore, this resembles the sinc function:
(D) Notice that the continuous set of slits forms a "top hat" transmission function. What is the Fourier transform of a top hat, and how does it compare to your sum from the previous step?
So the claim is that the continuous slits form a "top hat". Let's look at a diagram to show that this is indeed the case:
As we analyzed the relationship between the diameter of the top hat and the wavelength, you can think of the diameter as the diameter of the primary mirror in a telescope. As a result, the relationship in the previous part tells us that the larger the diameter is in a telescope, the more resolution it has.
The relationship to the angular resolution can be provided by:
\begin{align}
\theta \propto \frac{\lambda}{D}
\end{align}
which shows that the larger the diameter of the mirror, the more detail the from the diffraction bands of the wavelength can be gathered.
Wow... this problem really opened up my eyes as to how telescopes actually work!!
 |
| Figure 5: The Even Pair Function |
If you look at the double slit as allowing two beams of light that diffract as they enter the slit, you can see how it resembles the Even Pair function in the Fourier Transformations cheat sheet. And if you look at the Fourier transformation of the Even Pair function, you can see that it turns into a cosine function!
WOWW!!! That was a lot of work to do the first part of the problem. But now that we know how to use Fourier transformation, we'll be able to see other cool connections in how light behaves as a wave.
So as for the second question:
(B) Now imagine a second set of slits placed just inwards of the first set. How does the second set of slits modify the brightness pattern on the screen?
Just like the first problem, let's think about it conceptually before we let the Fourier transformation just give us the answer. Let's look at the diagram for this scenario:
 |
| Figure 6: There are two sets of slits. The outer set of slits is separated by distance $D_0$, and the inner set of slits is separated by distance $D_1$. |
A visual representation of the constructive and destructive interference is as follows:
Okay, so now we know that we can use Fourier Transformations to add functions together to represent even more complicated functions. That is going to be a very useful strategy for the next concept:
(C) Imagine a continuous set of slit pairs with ever decreasing separation. What is the resulting brightness pattern?
In this case, we are just dealing with an infinite number of slit pairs. Since we will be adding many different cosine functions together, we will have even stronger constructive interference in the center, and very strong destructive interference as you progress outwards from the center. Since only the center will continually have more and more constructive interference, thereby making it much brighter, while the outskirts away from the center will be a mixture of crests and troughs all over the place, the deconstructive interference will make the outer bands much dimmer. Therefore, this resembles the sinc function:
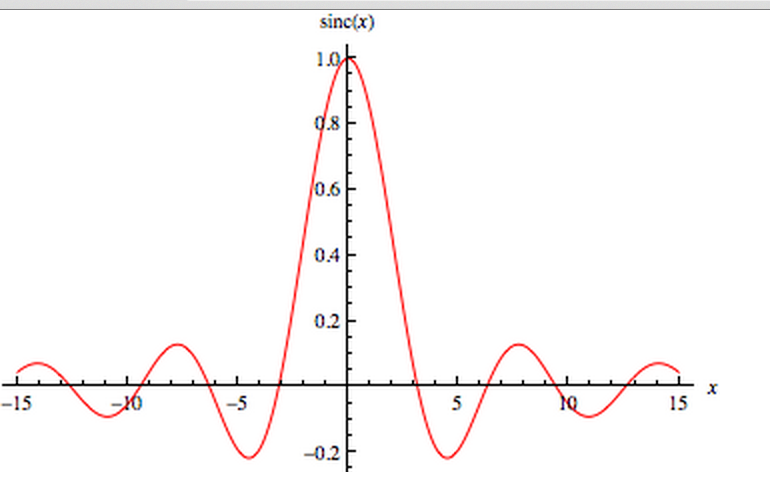 |
| Figure 8: Sinc Function |
So the claim is that the continuous slits form a "top hat". Let's look at a diagram to show that this is indeed the case:
 |
| Figure 9: Continuous slits create a top hat (look at it sideways)!! |
According to the cheat sheet in Figure 4, a Top Hat function Fourier transforms into the Sinc function! That is exactly what we got in our previous step!!!
(E) For the top hat function's FT, what is the relationship between the distance between the first nulls and the width of the top hat (HINT: it involves the wavelength of light and the width of the aperture)? Express your results as a proportionality in terms of only the wavelength of light $\lambda$ and the diameter of the top hat $D$.
Since the top hat is made up of infinitely many slits, we can break each slit down to be the size of the wavelength, $\lambda$. Therefore, the width, $W$ can be represented by $W = \frac{\text{distance}}{\text{wavelength}} = \frac{D}{\lambda}$. The Fourier transformation tells us that the distance to the first null is $\frac{1}{W}$, so the relationship between the first nulls and the width of the Top Hat is $\frac{1}{W} = \frac{1}{\frac{D}{\lambda}} = \frac{\lambda}{D}$.
(F) Take a step back and think about what I am trying to teach you with this activity, and how it relates to a telescope's primary mirror?
Okay, since we've done a lot of math, lets think as to what is the use of knowing how light diffraction with relation to the distances it travels teaches us about telescopes? You can think of a telescope's entire primary mirror as a light-collecting tool, or a large single slit. As a result, as the telescope sits and gethers light, it measures the diffraction pattern the light makes, which ideally makes a sinc function.
As we analyzed the relationship between the diameter of the top hat and the wavelength, you can think of the diameter as the diameter of the primary mirror in a telescope. As a result, the relationship in the previous part tells us that the larger the diameter is in a telescope, the more resolution it has.
The relationship to the angular resolution can be provided by:
\begin{align}
\theta \propto \frac{\lambda}{D}
\end{align}
which shows that the larger the diameter of the mirror, the more detail the from the diffraction bands of the wavelength can be gathered.
Wow... this problem really opened up my eyes as to how telescopes actually work!!



Great post! I'm a big fan of the diagrams.
ReplyDelete